コンデンサ
基本問題解説
必須問題 a. c. d. e.
標準問題 b. f.
間違えが多い場合は、
解説を読み、
コンデンサの電場を
主にした解き方を
理解しましょう。
a.
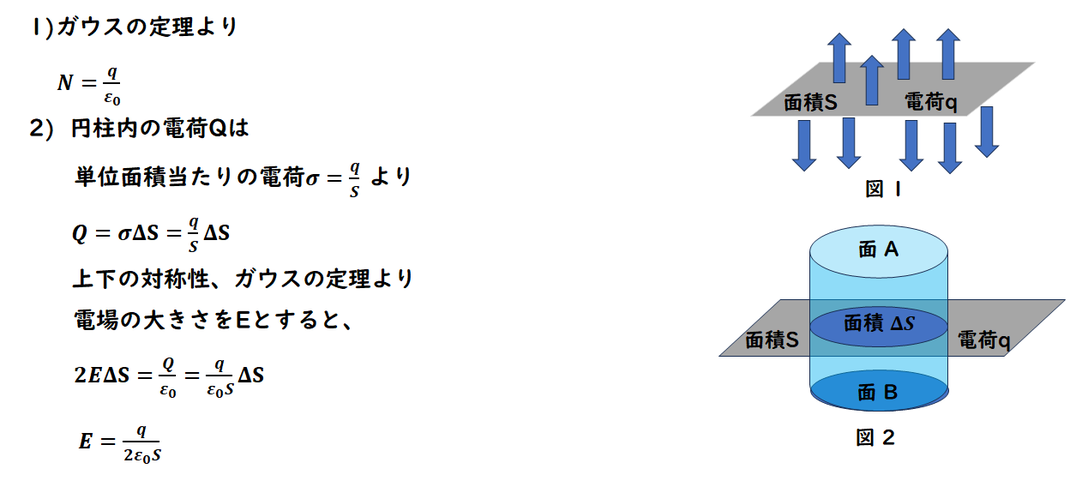
ガウスの定理による
電場の計算
コンデンサの
基本量を
求める問題です。
この問題を止まることなく
まずは、
できるようにしましょう。
電位と電場の復習問題です。
よくわからない場合は
もう一度
電位と電場の演習をしましょう。
極板の電場が求まります。

2つの極板を平行に
おいて平行板コンデンサを
作ります。
1個の極板が作る電場は 2)で求めました。
-qが作る電場は、極板に入る向きになります。
図のように向きを考えると、
コンデンサの中の電場の大きさは
下向きE+E = 2E
外側はE-E = 0
になります。

5) 電位と電場の関係
電場は一様なので、
そのまま
電圧 = 電場×距離
になります。
6)電気容量の定義
q=CV より求まります。
7) 静電エネルギーの公式
から計算します。
赤字の項目は暗記してください。

8) 極板Bの電気力は
コンデンサの電場ではなく
Aが作る電場による力です。
Aが作る電場は、2)で求めたので
F = qE になります。
b.

金属板の内部電場の大きさ=0を利用する問題です。
電荷からの作られる電場に
慣れましょう。

金属板の電荷が作る
電場の大きさはa.
などの復習です。
距離に関係なく一定
なので、
電場の図を描きます。
金属内部の電場=0
問題よりQA+QB = Qを
利用して
電荷を求まることができます。
電場の大きさは外側は
ともに同じ向きなので
大きさも同じです。
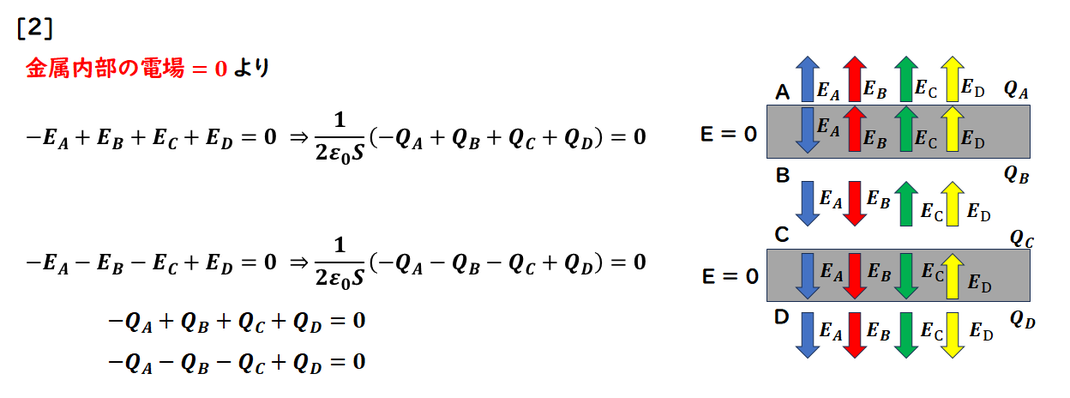
1)を組み合わせた問題です。
1)と同じように、
電場の図を完成させて、
金属板内部の電場=0
により、2式完成します。
2),3)は与える電荷が違うだけで
ここまでは同じです。
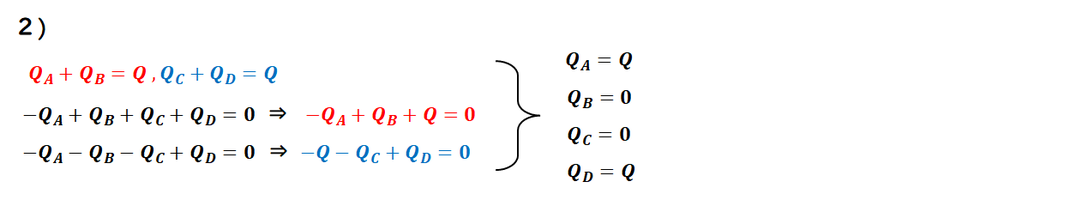
与えられた電荷を
金属板電場=0からの式
に入れて解くことになります。
式の赤の組、青の組で
それぞれ各電荷が求まります。
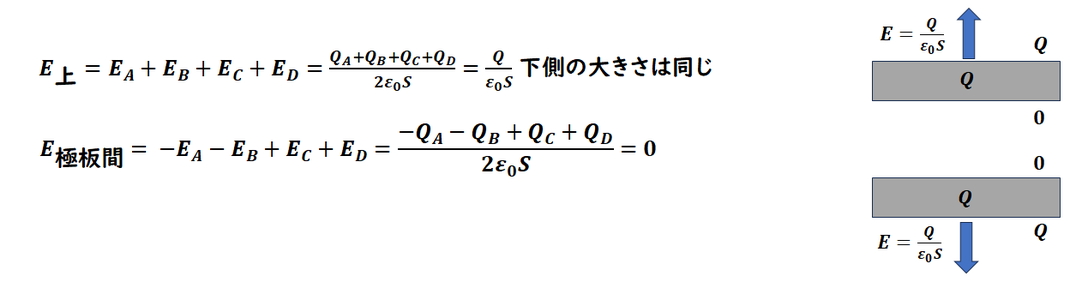
図の向きなど
間違えないように
計算して電場の大きさを求めます。
3)は2)と
初期の与える電荷が違うだけで
計算方法は、同じです。
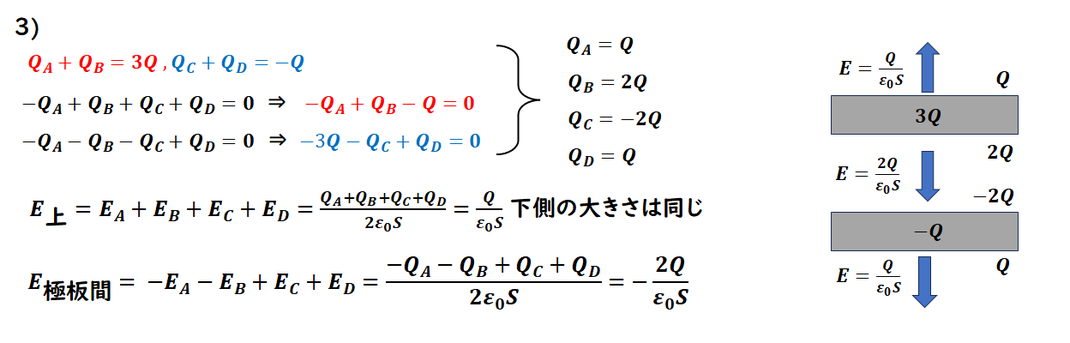

すべての電荷を
考えると難しそうなのですが、
よく見ると、
変化しているのは、
内部だけなのに
気が付けば
解くことができます。
これは、
コンデンサの
初期電荷0から
2Qになった時と
同じ状況なので、
外力の仕事=ΔU
静電エネルギーの変化
により、
静電エネルギーの変化を
計算すればよいことになります。
電気容量などなく、
初期0なので、
ΔU = 1/2 (2Q)V ―0
になります。
V = 電場の大きさ×距離から
求めてWが
求まります。
電場の大きさを
理解していないと、
解くことは難しく、
かなり差がつく
問題だと思います。
数回演習すれば
それほど難しくは
ないです。
c.

充電時の電荷、電場の大きさを求めておきます。
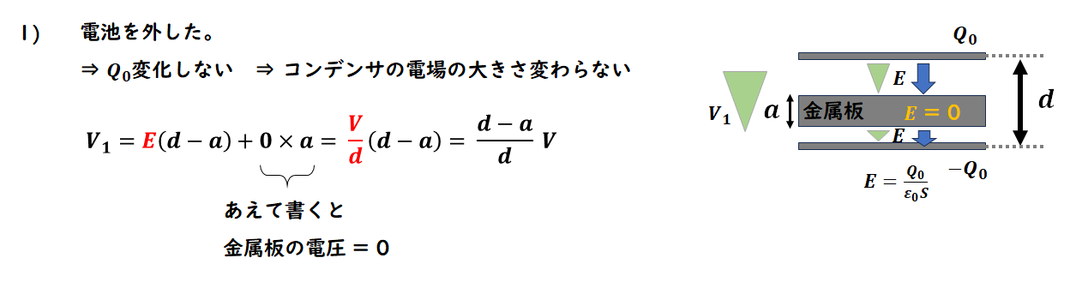
金属板の電場の大きさは0、
電荷は変わらないので、
電場の大きさも変わりません。
金属板の電圧は0になり
コンデンサの電圧が求まります。

1)の電圧から
電気容量を求めます。

1),2)とほとんど同じで
求めるものが変わっているだけで
内容は同じです。
コンデンサが変わって
再度電圧Vにするので、
電荷が変わります。
電場の大きさも変わります。
電気容量を2)で求めたので
電荷は求まります。
電場の大きさは1)同様です。
d.
電気容量の公式で
求めることはできますが
電場の大きさで
求めてみましょう。

c.と同じように
電源をはずす
方法で求めてみます。
電源をつけたままを想定しても
良いです。
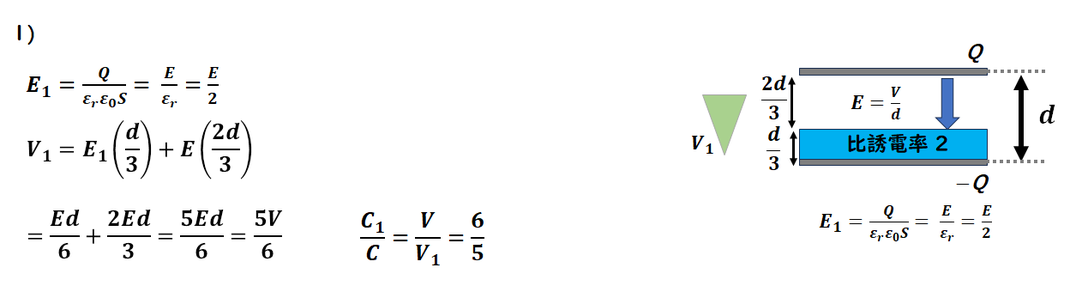
電荷の変化がないので、
電場は同じです。
誘電体のところは、
誘電率分小さくなります。
電場が求まり
電圧を求めます。
電圧比から計算します。

左右に分かれる場合は、
電荷を左右に分けます。
総電荷は変わりません。
Q = Q1+Q2になります。
電荷は異なりますが、
電位と電場の大きさの関係より
左右の電場の大きさは同じです。
Q1とQ2の関係式が求まります。
各電荷が求まり
電場の大きさが求まります。
電場の大きさから
電圧が求まり
電気容量が求まります。
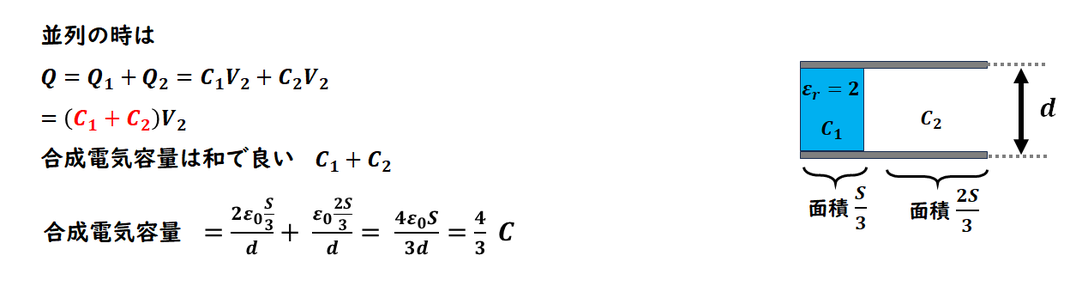
並列時は計算がやや
面倒になります。
合成容量であれば
Q = Q1+Q2
はわかっているので、
各電気容量の和に
なるので計算できます。
同様に、
直列の時も
言えますが、
直列の場合、
電場の計算方法は
和になるので
簡単になります。
おすすめは、
直列は電場
並列は電気容量
で行くのが
効率が良いです。
c.の問題は
電気容量の計算で
行うと面倒だと
思います。
やっていませんが。
電気容量の公式
だけ覚えても
ほかの問いに
まったく
答えられないので、
電場の計算が
十分できてから
効率を求めるように
してください。
入試の問題は
電気容量の公式
だけ覚えても
時間をかけさせる
問題が多く、
電場の計算を
させる問題が
よく出題されます。
e.


V一定で計算します。
電荷変化なので、
電場も変化します。

電池を切る場合は、
電荷は変化しません。
電場の大きさも変化しません。

2)とほぼ一緒です。
金属板部分は
電場0で等電位です。

3) と同じです。
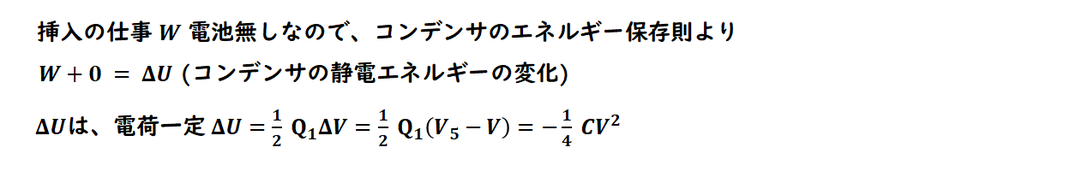
コンデンサのエネルギー保存則の演習です。
電池、抵抗なしなので、
外力の仕事=静電エネルギーの変化
です。
静電エネルギーは電荷一定なので、
電圧の変化から求めればよいです。
この問題が止まることなく
できれば、だいぶ電場の計算は
理解したことになると思います。
f.
誘電体の挿入する力を求める問題です。
流れはほとんど一緒で出題されるので、
問題数も結構あるので
得点源としては良い問題です。
必ず得点できるようにしましょう。
エネルギー保存則から
外力の仕事を求め
外力の力を求めます。
解答としては、
挿入時に
電場の力は挿入方向
外力は外側になることを
知識として
覚えておくとよいです。
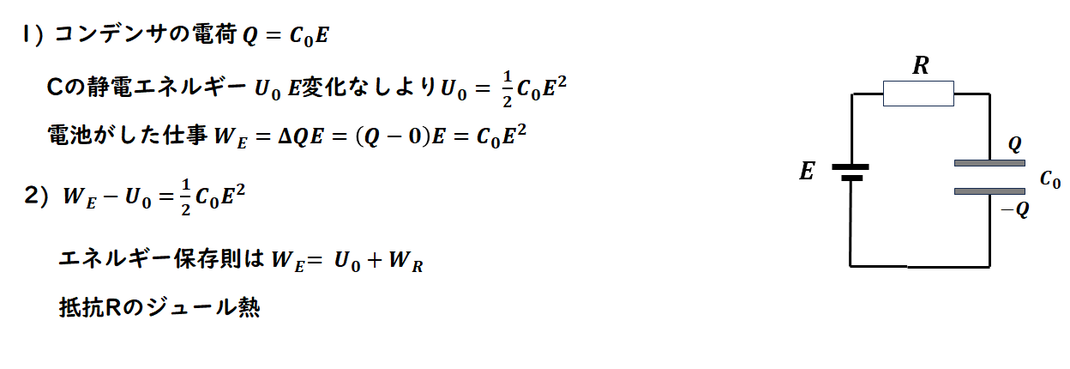
仕事、エネルギーの計算です。
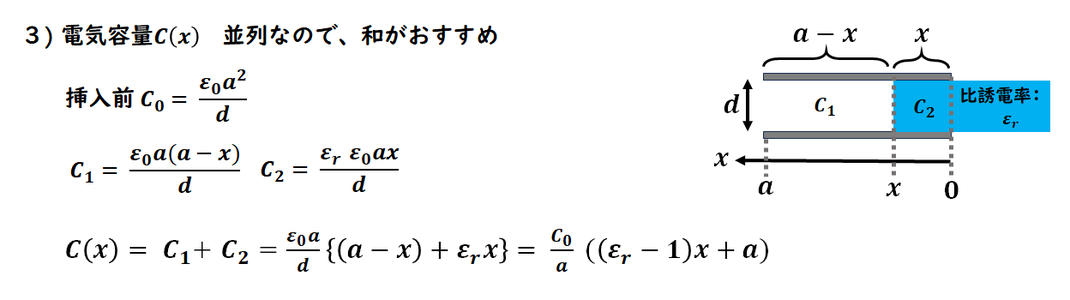
電気容量の式は基本的には使いませんが、
並列で、合成電気容量は?と
聞かれる場合は和で良いので
使います。
d,ε0が与えられてないので、
C0から求めます。
電場から求めるのも
計算演習としては良いです。
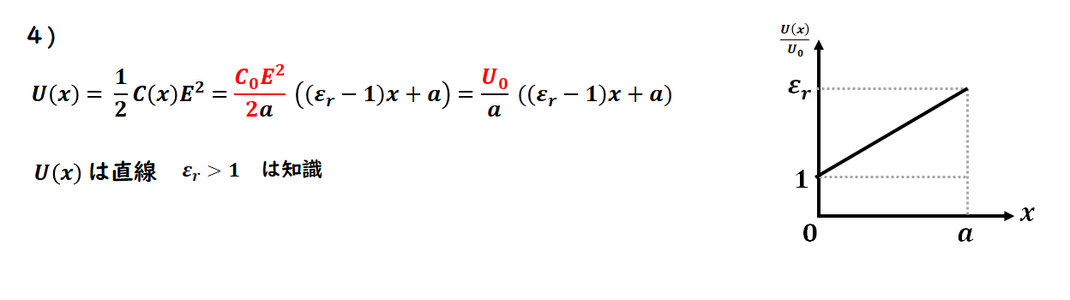
静電エネルギーを求めます。
そのままです。
グラフは、比誘電率は1より大きいので
グラフは上向きです。
覚えておくべき知識です。
電場は
弱くなることも覚えておきます。

エネルギー保存則です。
3つあることになります。
それぞれ求めていきましょう。
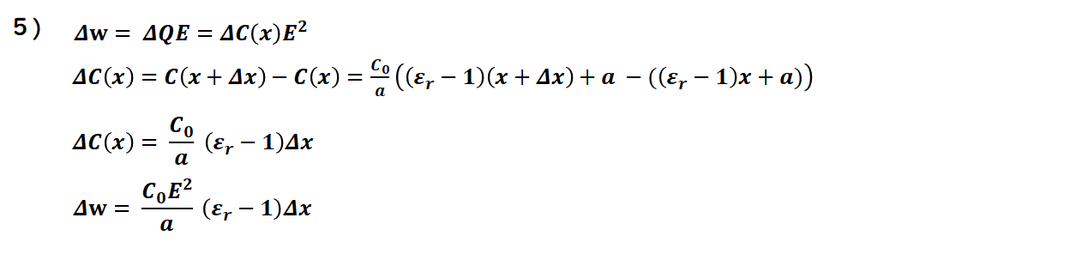
電池の仕事は 電荷の変化×電圧です。
電荷の変化= C'E-CE = (C'-C)E
です。
電気容量の変化になります。
計算結果に自信がない場合、
あくまで確認方法として
微分を使うことができます。
そもそも
f(x)の微分は
f'(x) = (f(x+Δx) - f(x)) / Δx
なので、
もちろん(Δx) ⇒0ですが
f(x+Δx) - f(x) = f'(x) Δx
いうことになるので,
ΔC(x) = C'(x)Δxと
なるはずです。
確かになっています。
(Δx) ⇒0が
書かれていないので、
計算しないといけないのですが
1次式の場合は成立します。
1次式以外は
(Δx)の式が出てくるので
そのままは利用できないですが
(Δx)⇒0として
とある場合は利用出来ます。
一応計算して確認で使うぐらいが良いです。
あと、Δx 書き忘れもあるので
あくまで計算確認ぐらいが
良いと思います。
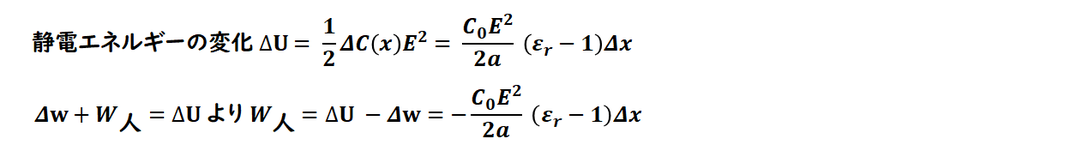
静電エネルギーです。
電圧一定なので、
1/2 CE^2の利用です。
結果的に
電池の仕事とほぼ同じになるので、
電池の仕事の結果を利用します。
エネルギー保存則より
外力の仕事を求めます。
予定通り、
負となり
引き出す方向になっています。
何度もやっていないと
不安になるところです。
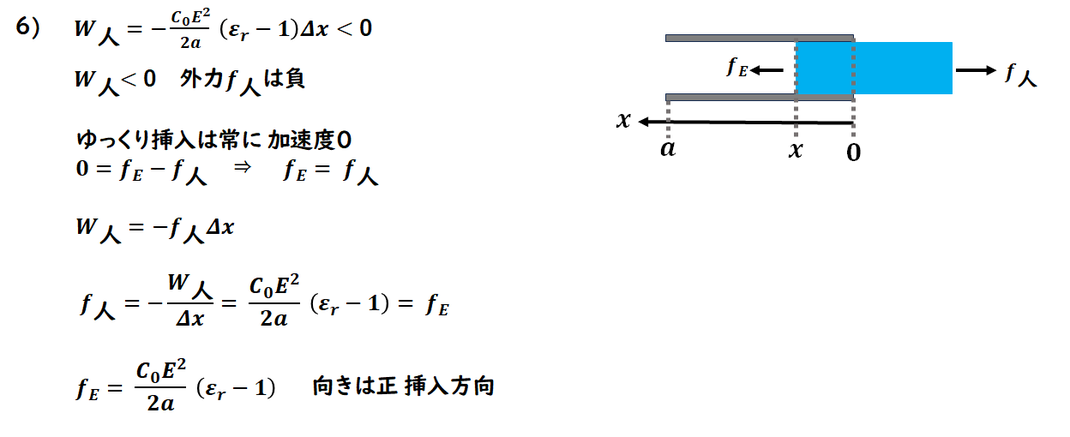
最終目標の力を求めます。
いろいろ書いていますが、
外力を出すのは
外力の仕事/Δx
です。
外力と大きさが同じで
逆向きが電場の力です。
両方とも出やすいので、
向きを間違わず、
力の大きさは?
向きも考慮して
求める場合などあるので
慎重に答えましょう。
流れは
ほとんど同じなので、
似たような問題をいくつか
やってみるとよいです。
標準に1問あるので
やってみましょう。
