電位と電場
電磁気では、似たような用語が多く登場します。
たとえば、
電位、電場、電気力線、
電圧、電位差、電流
電荷、電子
など、見た目が似ていて
混同しやすい単語が多数あります。
それぞれの意味を正しく理解し、
区別して使えるようにすることが大切です。
あいまいな理解のままでは、
問題を解く際に混乱してしまうことがあります。
まずは一つ一つの言葉が
何を意味しているのかを丁寧に整理し、
自信を持って使えるようにしましょう。
まずは
「電位」と「電場」から始めましょう。
「電位」「電位差」「電圧」「電場」
混同せずに、
正しく理解することが大切です。
このページは、
コンデンサの演習に向けた準備と
考えて取り組んでください。
基礎をしっかり身につけておくことで、
後の学習がスムーズになります。
1.電位
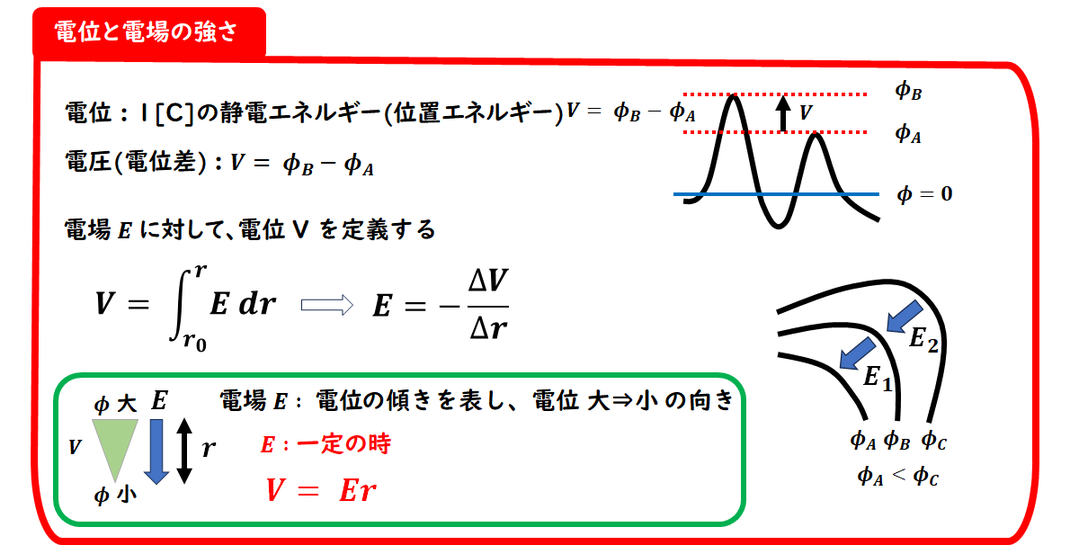
まずは、電位です。
力学で、似たようなものとなると
高さ方向の位置 Z位置になります。
電位は、基準からのエネルギーになります。
基準は、おおむね2通りあり、
無限遠、アースを0とします。
2つの異なる電位ΦA,ΦBの差(高さ)を
電位差ΦB-ΦAを電圧とします。
電圧:ΦB-ΦA (電位差)が、
高さとおなじとして覚えましょう。
電位を山の
等高線のようなものと
考えた場合、同じ電位を
結んだ線を等電位面といいます。
電位の勾配、傾きを表すベクトルが
電場です。
傾きが電場の大きさになります。
電場の向きは、
電位が大から小の向きが、
正となります。
これは、重力の向きと同じです。
力学的に対応させると、
電圧: 高さ h
電場: 重力加速度 g
で、近い関係にあります。
電場が、一定の場合
電圧 V = Ex
が、成立し、
xは電位差の距離
です。
2.電場の力、仕事

電位差により
電場がある空間に、
電荷をもつ物質をおくと、
電位が高い位置から低い位置に
物質は移動します。
山で、物質を置くと
低い位置に転がるのと同じです。
つまり、
電荷は力をうけることになります。
電荷の電場による力は
F = qE で表せます。
q > 0なら、電場の向きと同じです。
q < 0(電子など)は 電場の向きと逆で
電位が高い位置に移動します。
電位の定義は1 [c]の
位置エネルギーなので、
電荷qでは
U = qΦ
になります。
電場による
電位が低いほうに動く事を
仕事の関係で表すと、
WE(電場の仕事) = ―ΔU
(位置エネルギーの変化)になります。
これは、エネルギーと仕事の関係の事です。
位置エネルギーの変化なので、
経路に関係ない事を
忘れないでください。
つまり、電圧(電位差)だけを
考えればよいことになります。
電荷の速度が変化すれば、
運動エネルギーの変化になります。
人の力で、
静的に電位を変化させる場合の仕事は、
WE(電場の仕事)の奪うことなので、
W(人の仕事) = ΔU (位置エネルギーの変化)
と、なります。
説明として、考えるとややこしいですが、
放置すると、基準点0に行く。
何もしないと、底に転がっていくのを
人の力(逆の力)で
阻止するイメージになります。
問題をやる前に、
いろいろな物理量が
でてくるので
厄介なのですが
覚えましょう。
ここまでで、
電位、電場の問題を解いてみましょう。
用語、物理量に疑問が無い場合は、
ガウスの定理まで
覚えてから問題を解いてください。
3.ガウスの定理
ガウスの定理です。
あまり、学んでいない人も
いるかもしれません。
ガウスの定理を直接
問題として出題されることは
あまりないようですが、
コンデンサの問題で、高得点をとるには、
ここを無視することはできません。
存在と使えるよう、
理解しましょう。

ガウスの定理になります。
式としては
電荷の周りに電場がわき出すように
分布する事を表しています。
ある空間に電荷が閉じ込められている場合、
空間から出てきた電気力線の本数を調べると
電荷の量がわかることになります。
単位面積を貫く本数がEの大きさになるので、
総面積×Eが全体の本数になります。
感覚的にとらえるのは難しいのですが、
ここで、覚えておくことは、
電荷があり、
閉じ込める空間が決まれば、
電場の大きさも決まるということです。
例題をしてみましょう。
平面に電荷が分布している例です。
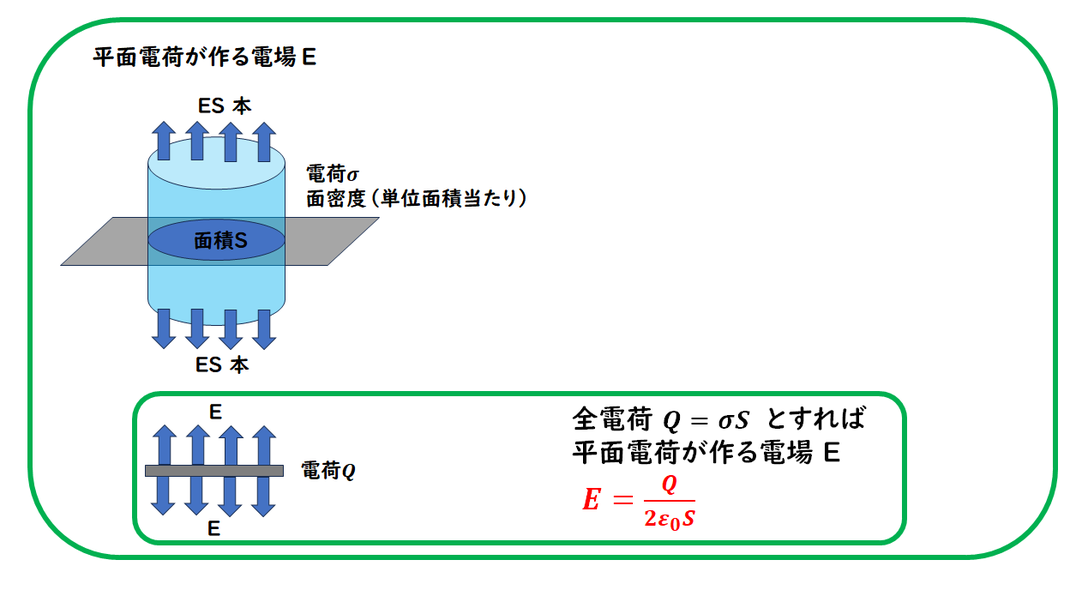
平面に電荷が分布する場合、
Z方向にのみ電気力線は
作成されます。
これは、上下均等になります。
この時に、
図のような円筒で平面を
閉じ込める領域を作り、
ガウスの定理をあてはめます。
閉じ込めた領域の電荷は
σが単位面積あたりの電荷の事なので、
Q=σSになります。
電気力線が出る本数を考えると、
単位面積当たりの本数がEの事なので、
上面はES本、下面はES本となり、
全部で、2ES本になります。
ガウスの定理の式にあてはめ、
E を求めることができます。
といった流れで、
電場の大きさを
求めることができます。
ガウスの式を覚えるのではなく、
ガウスの式から、電場の大きさを
出せることを覚えてください。
ここまでの演習を
実施してみてください。
次に、
コンデンサ演習を行います。
この項はコンデンサ演習への
準備と、とらえてください。
