波動の式

■ 波動を式で表す

 

波動は、グラフだけでなく

式でも表現できます。
基本的な操作や考え方は、

グラフのときと同じです。

 

■ 式の問題でよく出る内容

 

波動の式が関係する問題では、

以下のようなテーマがよく出題されます：

• 波の反射

• 進行波・反射波の合成

• 定常波の式（合成波）

これらはまとめて理解しておくと、

得点源になります。

 

■ 難しそうに見えるけれど…

 

最初は少し難しく感じるかもしれませんが、
何回か演習すれば、

必ず理解できるようになります。

 

グラフと対応させながら式を扱うことで、
「波の振る舞い」が

イメージしやすくなり、

式の意味もつかみやすくなります。

 

✅ アドバイス

• 「式とグラフを対応させて理解する」ことが大切

• 「波の向き（右進・左進）や時間変化」を式で表すことを意識する

• 定常波・反射波などのパターン問題は慣れがカギ！

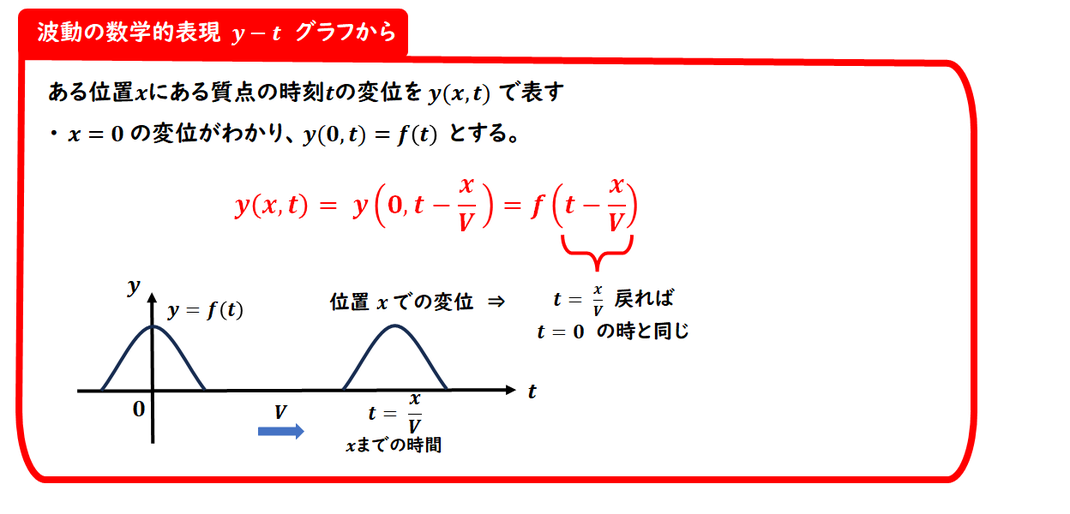
■ 任意の位置での

時間変化を求めるには？

 

ある基準の位置（たとえば$x=0$）での

時間変化 $y(t)$がわかっているとき、
任意の位置$x$ における波の変化は、
「その波が$x$ まで進むのに

かかる時間（遅れ）」

を考えて求めます。

 

■ 進行による時間のズレを考える

 

波が速さ$V$ で右向きに進むとすると、
位置$x$ に波が到達するのは、
時間 t0=x/V秒後です。

したがって、
位置$x$ における変位は、
「元の波を t0 だけ遅らせたもの」

になります。

 

■ 波動の式：y(x,t) の

表記に慣れよう

 

波の変位を式で表すときには、

次のように位置と時間の

両方を変数とする表記を使います：

y(x,t)：

x：位置（どこで）

t：時間（いつ）

 

つまり、「ある場所で、ある瞬間に、

波がどれだけ変位しているか」

を表す関数です。

 

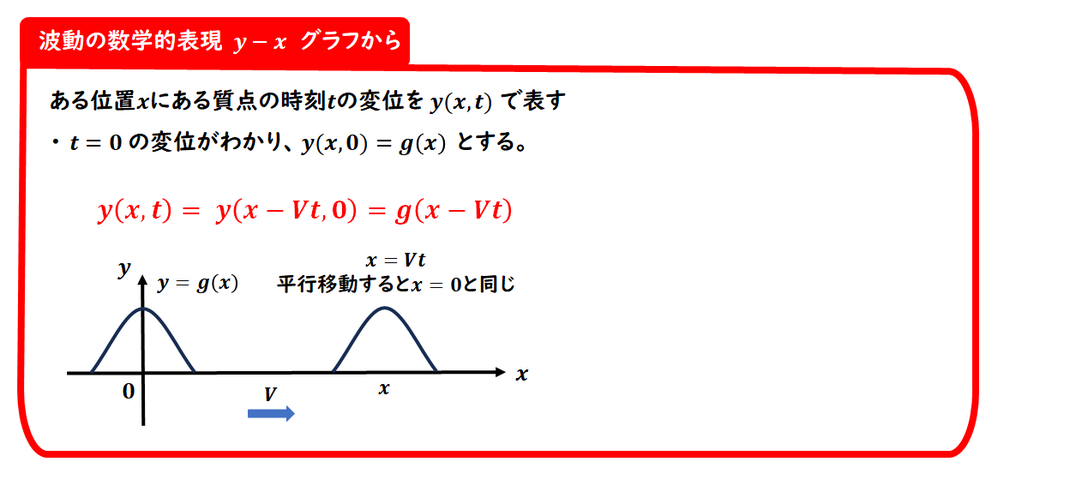
■ x=0での y–x グラフが

与えられたとき

 

波の時刻 t=0 の

y–x グラフ（波形）が与えられたとき、
その波が右向きに速さ$V$ で

進んでいるとすると、
任意の時刻 $t$ における波の形は、
「波形が右に $Vt$ だけ平行移動した形」

になります。

 

■ 基本の考え方

 

波は右向きに進むので、
時間 t 経つと、

波形全体が右へ $x=Vt$ だけ進みます。

 

このとき、位置$x$ における変位は、
もともと 位置 $x-Vt$ にあった波形と

同じになります。

 

■ つまり式では？

 

時刻 t における波の変位は：

$$y(x,t)=y(x-Vt,0)$$

 

これは、x=0 での波形を

右に Vt だけずらしたという意味です。

 

■ 覚えることは、これだけ！

 

波動の式の考え方は、
「進む向きにあわせて

時間や位置をずらす」という
基本ルールを覚えてしまえば大丈夫です。

 

あとは実際に問題を解いて、
理解を深めるだけです。

 

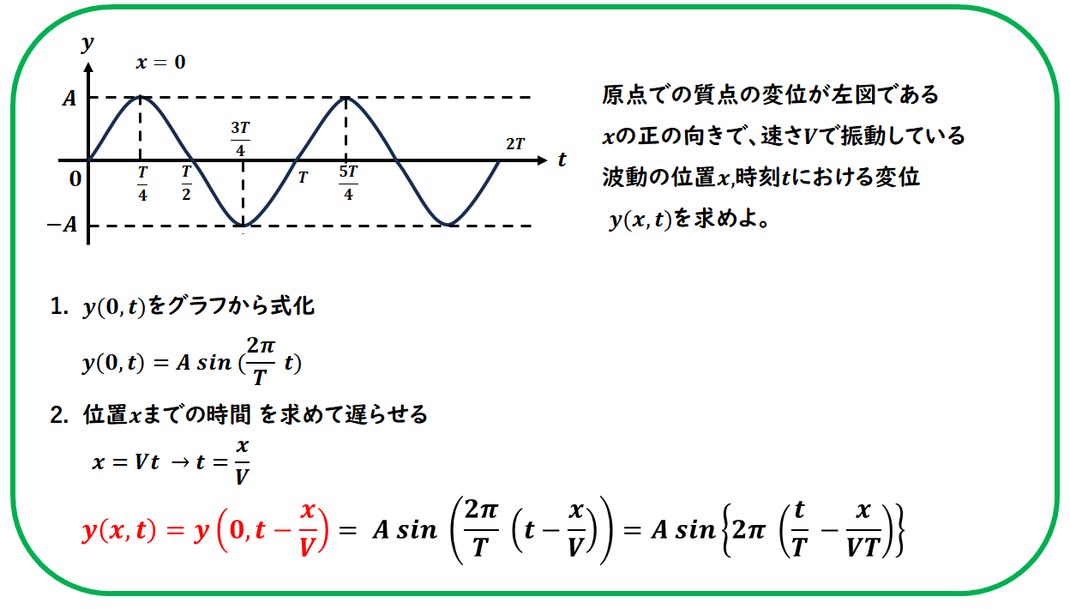
例題で確認してみましょう

 

ある点（x=0）での

y–t グラフ（時間変化）が

与えられたときに、

任意の位置x における

y–t グラフを求める問題です。

 

今回のグラフは、

横軸が「時間」になっているので、
これは "y–t グラフ

（時間変化のグラフ）"です。

 

問題文に「原点での」とあることから、
このグラフは、位置 $x=0$ における

変位の時間変化、
すなわち、y(0,t)を

表しています。

 

波動を式で表すときは、
位置$x$ と時間$t$ を変数とした

y(x,t)で表すとy(0,t)です。

まず、与えられた y–t グラフから、
以下の情報を読み取りましょう。

• 振幅 A
• 周期 T
• 波の形（関数の種類）
• → このグラフは sinカーブ 

T→２πを表すので、

1秒では、 2π/T となり、

t秒では、2π/T *t  が位相となり

解答になります。

 

2)

今度は、任意の位置$x$ における

波の式を求めます。

x = Vt より t = x/V 先にいます。

x=0で表現するには、

t = x/V 分遅らせ

y( x,t ) = y( 0,t- x/V)

で、求めます。

 

t - x/V をそのまま

代入して計算します。

 

■ よく出題される考え方

 

波動の式に関する問題では、
次のような「ずらし」の

操作がよく出題されます。

 

■ 基本の操作はこれ！

1.任意の位置 x における式

　　を求めるときは：

　　　　→ 波が到達するまでの時間

        　　　 x/V を「引く」

 

2.ある時間におけるグラフ

 （y–x グラフ）をずらすときは：

　       → 位置をずらす

            （波を平行移動）

       

   たとえば、t=0 の y–x グラフから、

   時間t における波を描くには：

      x→x−Vt に置き換える

   （波を右に Vt 平行移動）

 

■ 操作の覚え方

 

・「時間をずらすときは、

　　位置の分だけ遅らせる（引く）」

 

・「位置をずらすときは、

　　波が進む方向にずらす（足す・引く）」

 

波動の式においては、

　「時間を引く」 or

 「位置を引く（もしくは足す）」

　という操作を、

　波の進行方向に応じて行えばOKです。

 

この考え方を理解しておくと、
グラフ・式・定常波・反射の問題に

一貫した方法で対応できます。

 

■ 波の式の問題は「反射」と

セットで出題されやすい！

 

波の式に関する問題では、
反射の知識とセットで出題されることが

非常に多いです。

したがって、

反射の基本ルールを

しっかり押さえておきましょう。

 

■ 反射の2つのタイプ

 

波が端で反射するとき、

反射の仕方には2通りあります。

◎ 固定端反射

• 端が動かない（固定されている）

• 反射波は上下が反転する（位相がπずれる）

• 反射点の変位は常に 0

◎ 自由端反射

• 端が自由に動ける

• 反射波は上下反転しない（位相はそのまま）

• 反射点の変位は最大になることもある

「自由端」「固定端」という

名称の意味を知っていても、
それだけでは問題は解けません。

 

物理の問題では、

次のような

波の振る舞いを理解・記憶することが重要です。 

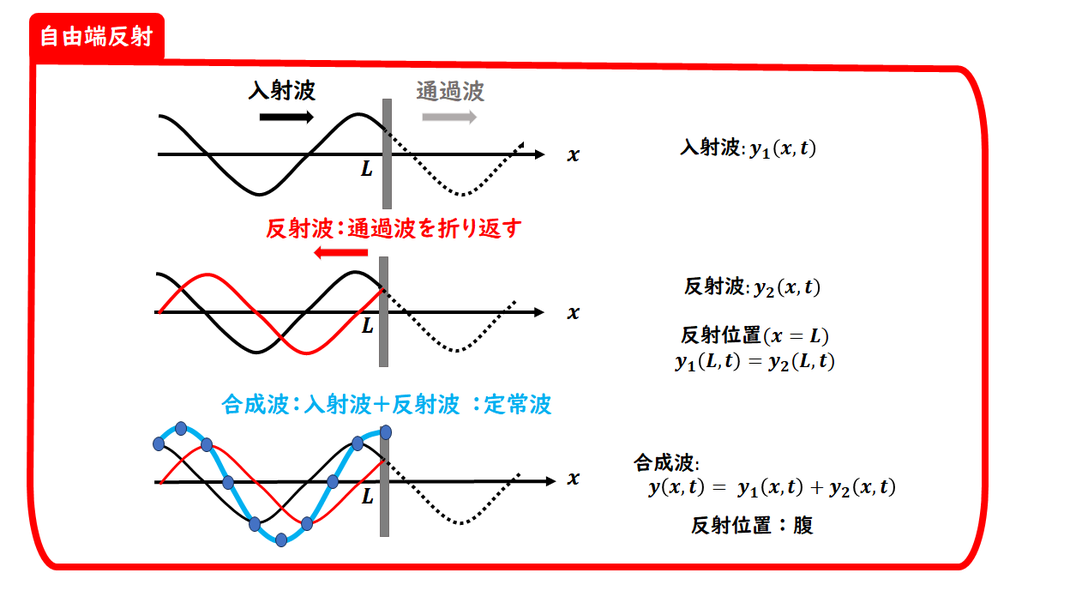
■ 自由端反射：位置$L$ での反射

 

波が右向きに進み、

位置 $x=L$ に自由端があるとき、
その壁で波は自由端反射を起こします。

 

■ 通過波と反射波

 

波がそのまま通過したと

仮定して描いた波を

「通過波」と呼びます。

自由端反射では、
この通過波とまったく同じ形の波が、

点 $x=L$ で反射波として戻ってきます。

※ 上下反転せずに返ってくるのが

自由端反射の特徴です。

 

→ イメージしやすい反射です。

 

■ 合成波

（入射波と反射波の重ね合わせ）

 

入射波と反射波が重なると、
それらの変位の和をとって

「合成波」ができます。

 

位置$x$ における合成波の変位は、

入射波の変位+反射波の変位で計算できます。

もし、どちらかの波が $y=0$ なら、

もう一方の変位がそのまま合成波になります。

 

■ 合成波の分類

• 進行波：同じ方向に進む2つの波の合成波（例：入射波＋通過波）

• 定常波：逆向きに進む同じ波（周期・波長・振幅が等しい）の合成波

 

■ 定常波の特徴

 

定常波では、

波が動いていないように

見えるという特徴があります。

• 節（ふし）：振幅が 0 になる点

• 腹：振幅が最大になる点

これらは、波長 $\lambda$ に対して：

• 節と腹は$\lambda /4$ ごとに交互に存在します。

■ 自由端反射のときのポイント

• 反射点（端点）は「自由に動ける」ため、腹になります。

• よって、位置 $x=L$ は振幅が最大になる点（腹）です。

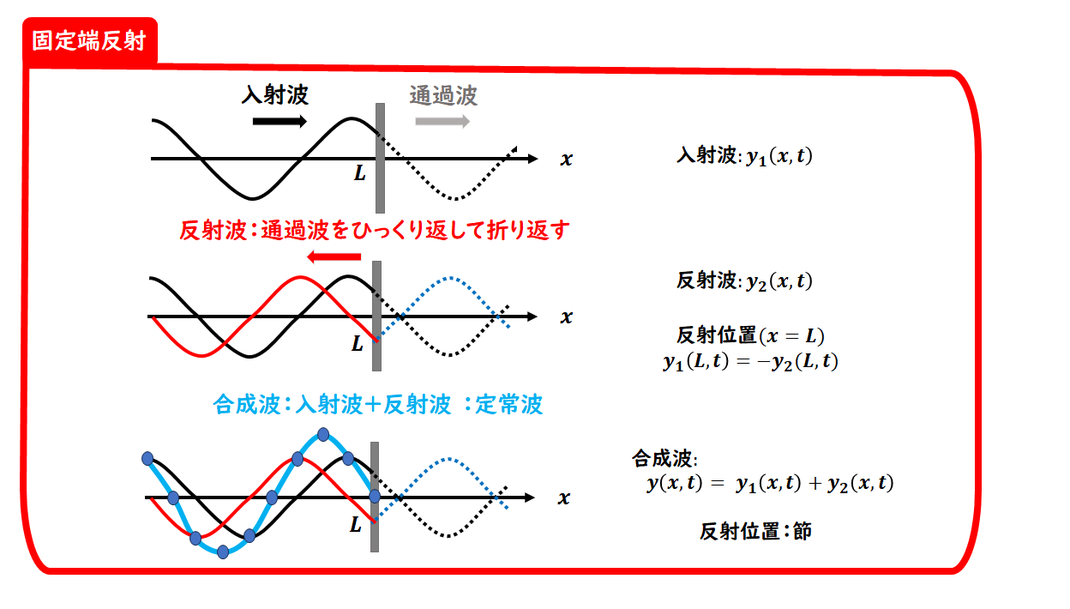
■ 固定端反射：位置$L$ での反射

 

波が右向きに進み、

位置 $x=L$ にある固定端で

反射される場合を考えます。

 

■ 通過波と反射波

 

波がそのまま進んだと仮定して

描いた波を「通過波」と呼びます。

固定端反射では、

この通過波を

上下反転（変位を -1 倍）

させた波が「反射波」になります。

• 通過波：入射波と同じ波

• 反射波：通過波を上下反転させた形（y → -y）

これは、

固定端では変位が常に 0になる

（＝動けない）ことを考えると自然です。

 

■ 合成波と定常波

 

入射波と反射波が重なってできる波を

「合成波」といいます。

 

この合成波は、周期・波長・振幅が等しく、

逆向きに進む波の合成になるため、
定常波になります。

 

■ 固定端反射の特徴

　・固定されている端（反射点）は、

　　動かないので

　　→ 常に変位が 0（節）になります。

 

　・節と腹（振幅最大の点）は、

　　波長λ に対して： 

　　・節：動かない点（振幅0）

　　・腹：最大に振動する点（振幅最大）

　　・節と腹は λ/4 ごとに交互に現れる

 

固定端反射は、教科書・問題集でも

作図問題としてよく出題されます。

 

次のようなステップで描けるようにしておきましょう：

1.通過波を想定（上下反転前）
2.通過波を上下反転して

   反射波を描く（左向き）
3.各位置での変位の和をとって、

   合成波（定常波）を描く

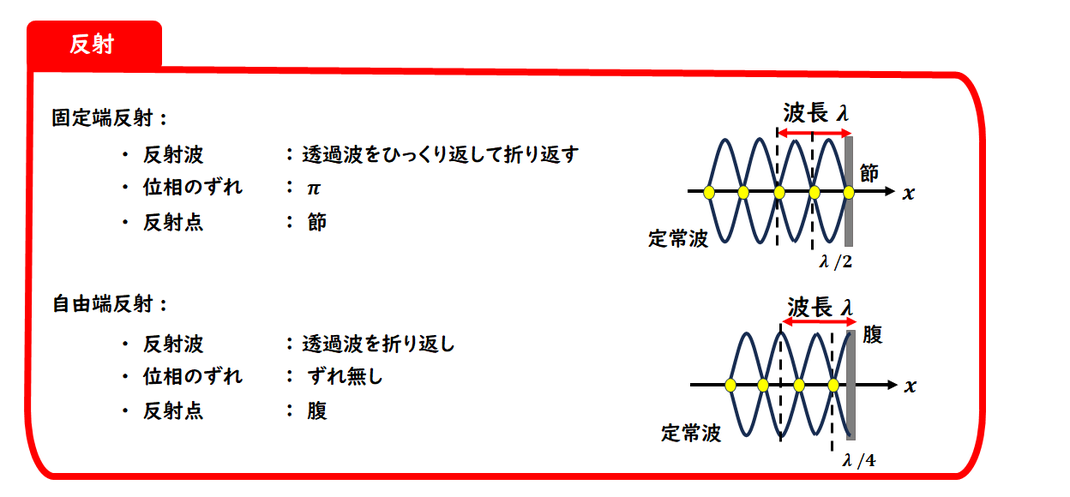
■ 反射に関する重要なポイント

 

波が端で反射する場合、

端の状態によって波の振る舞いが変わります。
特に、固定端反射と自由端反射では、

波の向きや符号、位相のずれに

違いがあります。

 

● 固定端反射のとき

 

・反射点の変位：常に 0（動けない）

・反射波は、上下反転（符号が逆になる）

・数式で表すと、位相が π（180°）ずれる

　つまり、sin(θ)　→　

　−sin(θ)　=　sin(θ+π)

　または sin(θ−π) としても同じ意味です。

 

📌 作図では上下反転、

式では「位相を π ずらす」と覚える！

 

● 自由端反射のとき

 

・反射点は動ける

　（反射波は上下反転しない）

・位相のずれは なし

・数式では、

　反射波はそのまま使う（符号変更なし）

 

● よく出る問題のパターン

• 「反射点から最初の節（または腹）の位置は？」

• 「定常波の節が何個あるか？」

• 「ある点が節になるための条件（長さと波長の関係）は？」

 

👉 波長 $\lambda$ と、波が伝わる範囲（長さ）が

与えられたら、
節や腹の個数・位置を

簡単に計算できます。

 

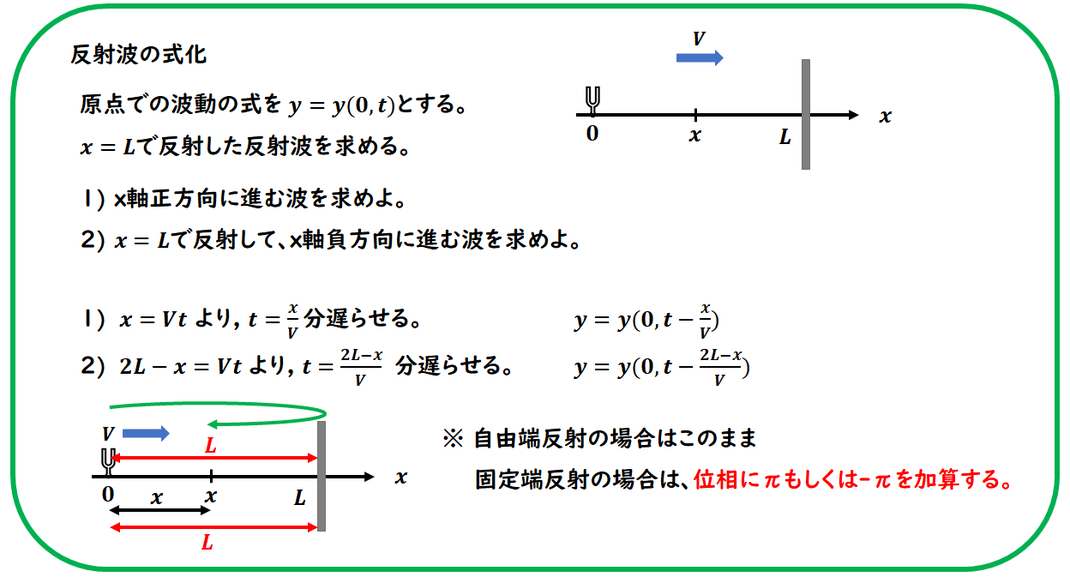
波動の式化において、
反射に関する問題は必須事項のひとつです。

 

特に、反射波および合成波（定常波）の式を

導出できることが重要となります。
これは頻出かつ得点源となるため、

確実に身につけておきましょう。

 

しっかりと理解しておけば、
出題された際に確実に

得点できる分野になります。

 

最初は難しく感じるかもしれませんが、
何度か演習を重ねることで

決まった操作として自然に身につきます。

 

例題で説明することにします。

入射波、反射波の式化の問題です。

1) 入射波は、式化でやった事柄になります。

 

2) 反射波の式化です。

対称位置からやる方法もありますが、

折り返しがわかりやすく思えます。

1)同様に考えます。

 

Lで折り返して、

位置xに行くまでの時間を求めます。

距離が 2L-xなので、時間が求まります。

その分遅らせればよいことになります。

 

忘れやすいのが、固定端の場合、π足します。

ひっくり返しての操作になります。

 

うっかり忘れやすい部分なので、

しっかり意識しておきましょう。

 

さらに波を具体的な形式にして

合成波を実際に式化します。

1),2)は実際に解いてみてください。

3)を考えてみてください。

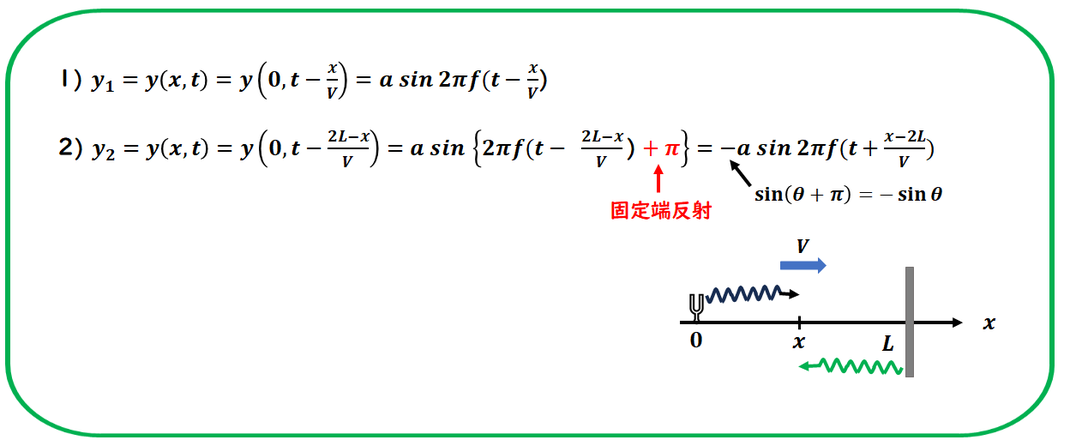
以上になります。

ずれのπを

忘れないようにしてください。

3) 合成波の計算です。

そのまま足します。

 

このままだと、定常波に

なっているかわからないので、

ここから積の形にします。

 

三角関数の和⇒積の公式を

利用します。

数学処理なので、

後で説明します。

 

積の形にすると、

時間の項と位置の項に分かれます。

位置の項をA(x)とすると、

cosとA(x)の積の表現で、

波の式になっています。

 

この時のA(x)は、定常波の振幅になります。

振幅は正なので、絶対値になります。

位置による関数で、sinの関数なので、

 

位相が０とかπだと常に０になります。

ここが、節の位置になります。

 

また、π/２や3π/２だと最大値をなり

腹になります。

 

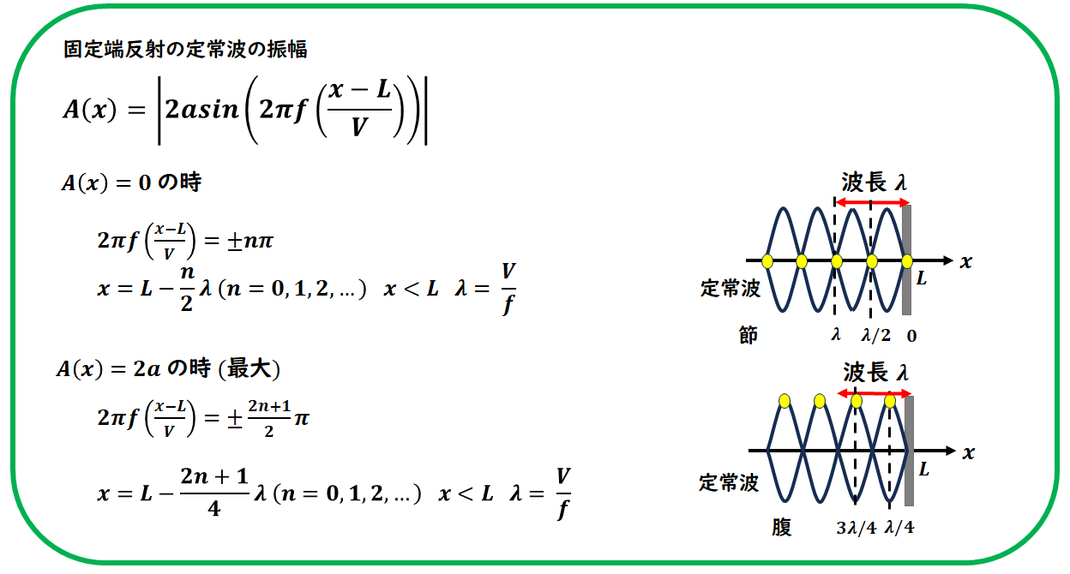
振幅の情報から、

節や腹の位置を求めることができます。
多くの問題では、

この段階までの計算や理解が問われます。

 

このレベルまでは、

確実に求められるようにしておきましょう。

 定常波の計算では、

非常に重要なポイントです。

多くの場合、問題文に記載されています。

 

そのまま使えばよいのですが、

混乱しやすく、

間違えやすい箇所でもあります。

そこで、以下のように整理して覚えておくと、

ミスを減らすことができるでしょう。

 

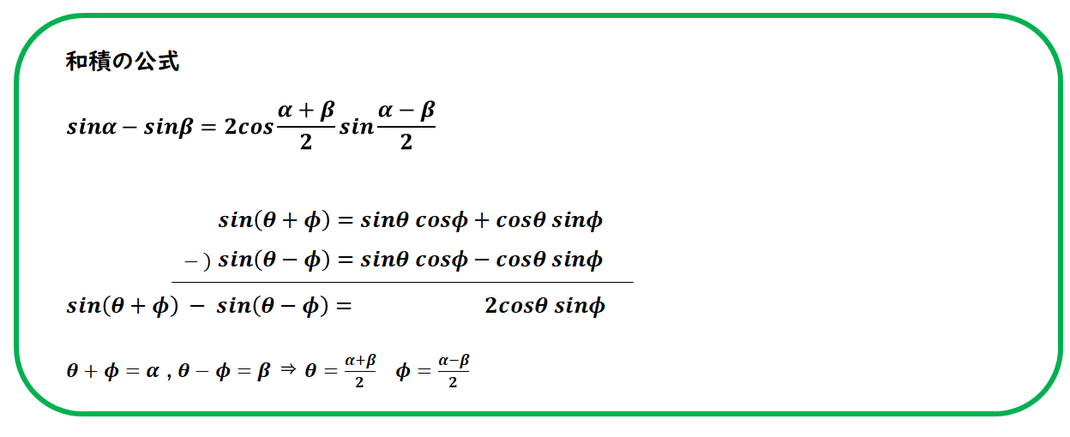
この公式は、

加法定理（sin・cos）の和や差から

導くことができます。
ただし、公式を丸暗記しようとしても、

忘れやすいので注意が必要です。

 

sin-sin,cos-cosで積が、

どのような式に変形されるのか、

イメージを持つようにしましょう。

また、この公式を使う際には、
(α + β)/2 や (α − β)/2 の計算が必要になります。

さらに、

式の前につく「2」を忘れやすいため、

意識して確認するようにしてください。 

(α+β)/2 , (α-β)/2を

それぞれ別々に計算してから

式に代入するようにしましょう。

 

このままでも問題ありませんが、

x の前にマイナスがつく形が気になる場合は、

符号（−）を前に出して

整理しても構いません。

計算ミスを防ぐために、

落ち着いてゆっくり書きながら

進めることが大切です。

 

また、定常波になる場合は、

x の関数と t の関数に分かれる形になります。
もし、そうなっていない場合は、

計算に誤りがある可能性が高いと

考えて見直しましょう。

 

・グラフと式　入門問題

・グラフと式　基本問題

・グラフと式　演習問題

 

波動へ