波動のグラフ

波を表現する際には、

グラフを用いることが

よくあります。
グラフを通して、

波を表すさまざまな

物理量を読み取ることができます。

グラフの種類には、

主に次の2パターンがあります：

y–t グラフ（時間と変位の関係）
y–x グラフ（位置と変位の関係）

それぞれ意味や読み取り方が異なるため、

しっかりと理解しておきましょう。

また、波には大きく分けて

次の2種類があります：

1. 横波

（変位の向きが波の進行方向と垂直）

2. 縦波

（変位の向きが波の進行方向と同じ）

特に縦波は見た目で理解しにくいため、
横波として表現して考えるのが一般的です。

この項目では、
波のグラフから読み取れる

物理量に関する問題演習を

行っていきます。

苦手な人は、

まず解説を読んでから

問題に取り組むとよいでしょう。

１．波動のグラフ

y-t グラフ

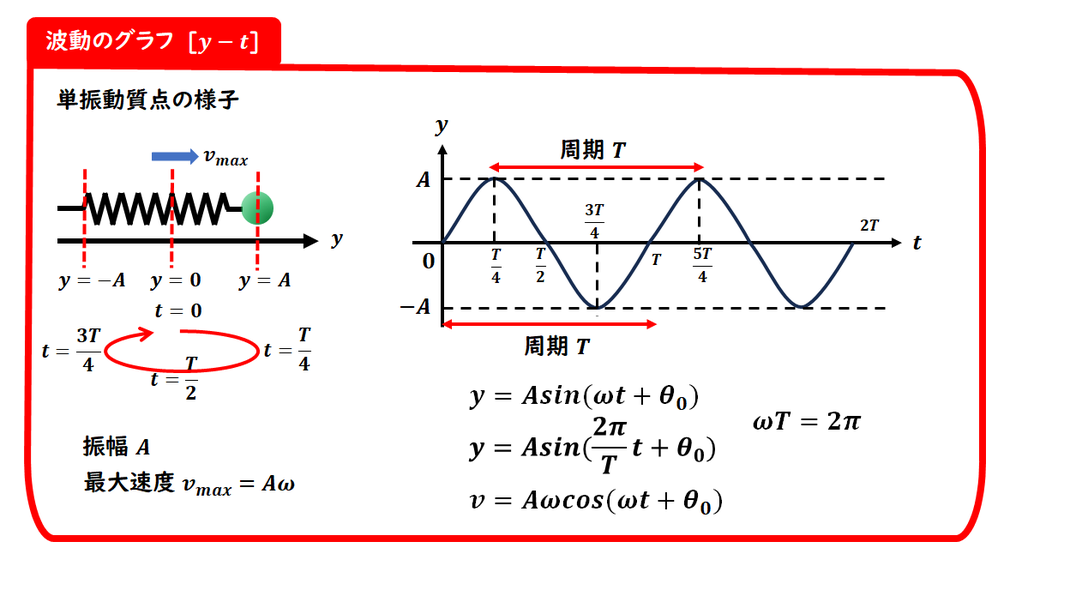
波のグラフは、

正弦波（sinやcosカーブ）で

表されることが多いです。

この項目では、y–tグラフについて説明します。

■ y–t グラフとは？

y–tグラフは、「ある1点の変位が

時間とともにどのように変化するか」

を表したものです。

横軸：時間 t
縦軸：変位 y

このグラフは、

単振動のグラフ（sinカーブ）として

考えると理解しやすいです。

■ グラフから読み取れる情報

1周期分の横幅は、周期 Tを表します。
縦軸の最大値・最小値は、"振幅 A（最大変位)"です。
y = 0 を通過する瞬間は、速さが最大になるタイミングです。

■ 単振動における速さ

単振動では、

変位の速さの最大値

（速さが最大になる瞬間の速度の大きさ）は

以下の式で表されます：

vmax = Aω

■ 注意ポイント

y–tグラフは、

時間の変化に注目するグラフです。
単振動と似た形をしているため、

感覚的にも理解しやすいかもしれませんが、
横軸は「時間」であるということを

必ず意識しておきましょう。

y-x グラフ

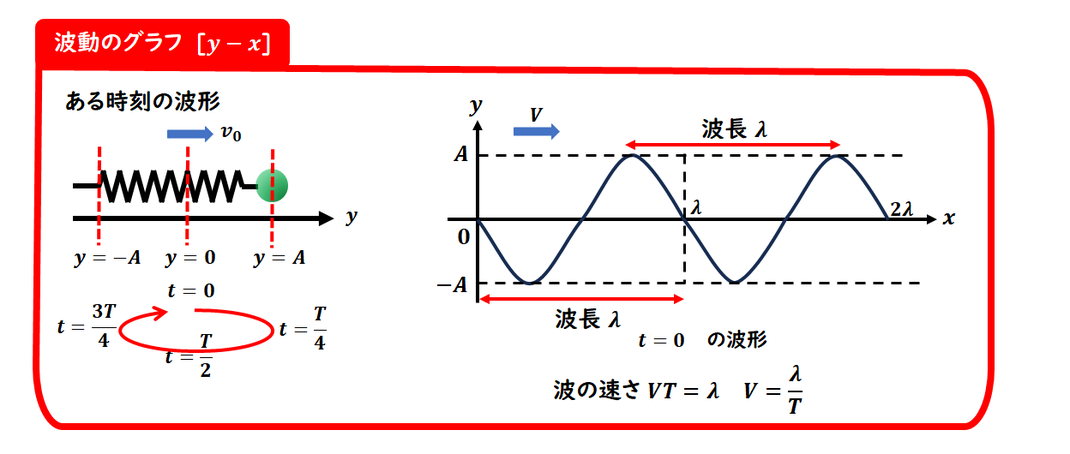
y–xグラフは、「ある時刻における

波の形（変位の空間分布）」

を表すグラフです。

■ y–x グラフとは？

横軸：位置 x
縦軸：変位 y

このグラフは、

t = 0に、各点がどのように変位しているか

を示しています。

■ グラフから読み取れる情報

1周期分の長さ（波の繰り返しの間隔は、波長 λ（ラムダ）です。
y軸の最大値・最小値は、振幅 Aで、最大（最小）変位を表します。

■ 波の進行方向に注意！

y–xグラフを読むときは、

波の進行方向がとても重要です。

例として、ここでは

波が右向きに進んでいる場合を考えます。
進行方向が異なれば、

同じ波でもグラフの形が変わって見えるため、

注意が必要です。

■ 波長と波の速さの関係

波の長さ（波長 λ）と速さ v、周期 T の関係は以下の通りです：
$λ = v T$

これは、

「1周期（T）の間に

波が進む距離が波長（λ）」

であることを意味しています。

■ 単振動との違いに注意！

波の速度 v は、「波そのものが進む速さ」
一方で、単振動における速度は、

「媒質の点が上下に振動する速さ」です。

この2つは全く異なるものなので、

混同しないようにしましょう。

■ y–x グラフに違和感を

覚える場合は…

y–tグラフを元にして、

y–xグラフが作られます。
そのため、最初は違和感を持つ人も

少なくありません。

違和感がない方は、しっかり理解できているので、次に進んでください。
違和感がある方は、次の説明でその違いをじっくり確認しましょう。

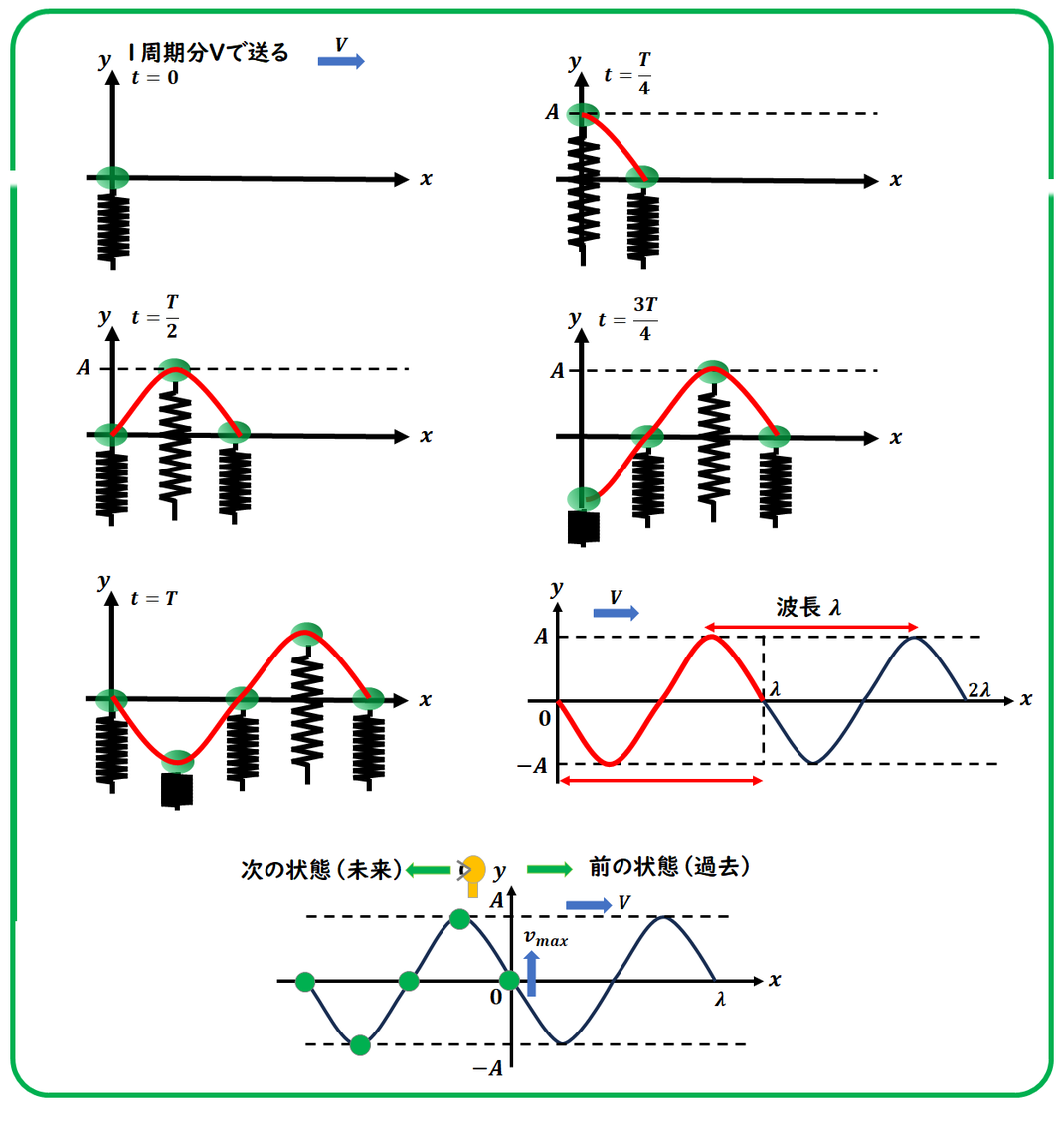
y–xグラフを理解するためには、

単振動の様子を時間ごとに

分けて考えるのが効果的です。

たとえば、

単振動する質点の動きを

周期 T を4分割（T/4ごと）に観察しながら、

右方向に波が進むように並べていくと、
その動きが空間に「波」として見えてきます。

これが y–x グラフの考え方です。

■ 「右が未来」だと、

違和感がある理由

y–xグラフを初めて見たときに、

「なぜこういう形になるの？」

と違和感を持つ人もいます。
その原因のひとつが、

「右側が未来」と考えてしまうことです。

実は、

"波は左からやってくる（右へ進む)"ので、

次の状態（未来の波）は左側にある

と考える必要があります。

■ 🎮 ゲームで考えてみよう！

横スクロールのシューティングゲームを

イメージしてみてください。
敵は左からやってくるので、

あなたが x=0 の地点で、
敵が上に現れるタイミングで

ジャンプして弾を撃てば、

T/4後にやってくる敵に命中できます。

この感覚をつかめば、
y–xグラフの「波の進み方」が

自然に理解できるようになります。

よく「波を少しずつずらして描く」

方法がありますが、
そんな必要はありません。

波は空間上の各点が“

ある決まった振動を時間差で

繰り返している”だけなので、
時間と位置の関係を正しく理解すれば、

未来の方向を考えれば、

次の位置が簡単にわかります。

■ ある位置での y–t グラフを描くには？

「x = 一定の位置での

y–t グラフを描く問題」では、
その位置の左側にある

y–x グラフの波形を、

時間の流れに沿って再現すればOKです。

つまり、波がその点に到達する順に

プロットしていけばよいということです。

まとめ

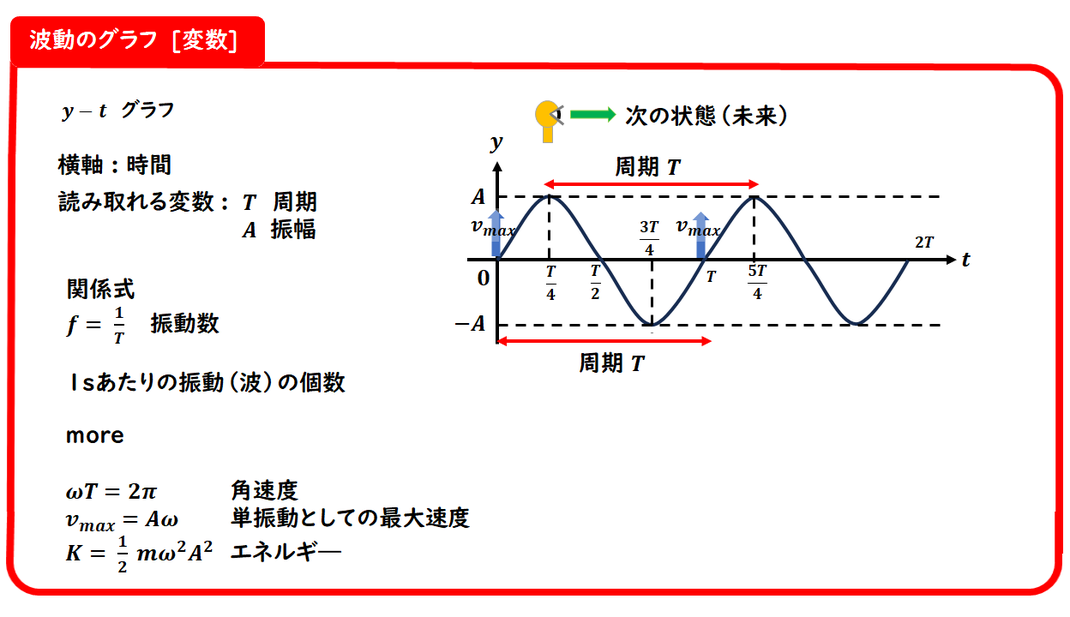
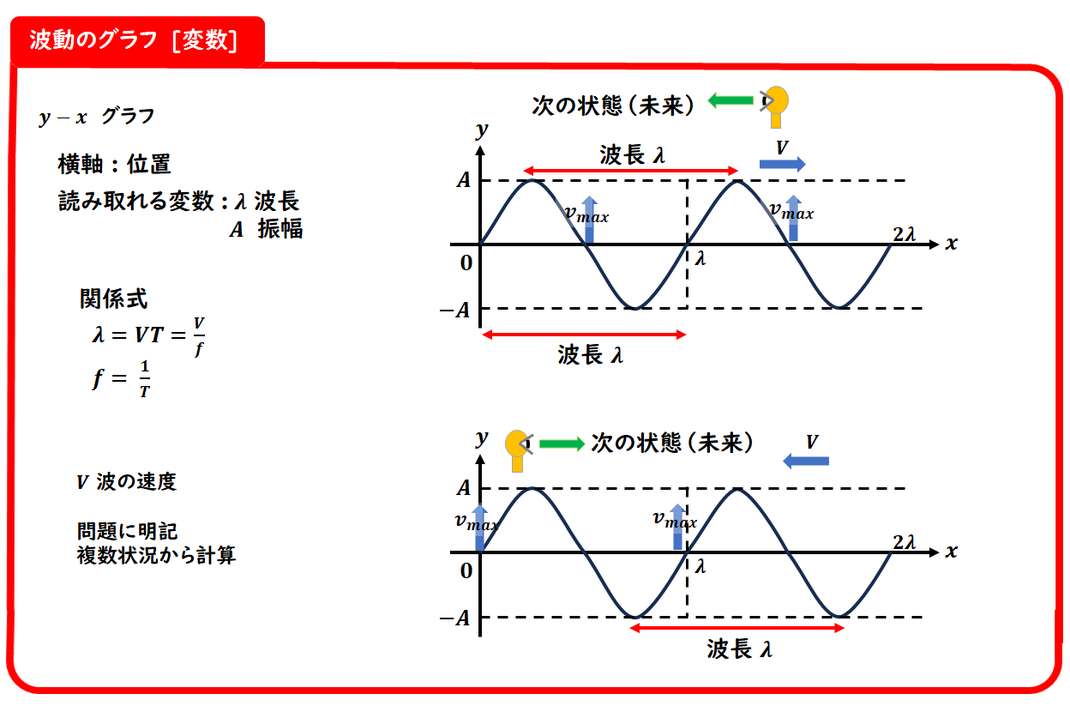
■ ここまでのまとめ

波を表すグラフには、主に2種類あります。
横軸が何を表しているかで、

グラフの意味が変わります。

① y–t グラフ（横軸：時間 t）

・「ある位置における

　変位の時間変化」を表します

・読み取れる物理量：

周期 T

振動数 f

② y–x グラフ（横軸：位置 x）

・「ある時刻における

　　　波の形（空間分布）」を表します

　・読み取れる物理量：

　　　波長 λ

　　　波の進行方向（→始点側が未来）

■ 重要な関係式

$λ = V T = V/f$

これにより、

波長・周期・振動数などの

物理量を計算できます。

■ 出題されるその他の物理量・内容

単振動に関する情報
- 角振動数 ω
- 質点の最大速度：
エネルギーに関する問題
- 振幅 A
グラフを描かせる問題
- 時間や進行方向を意識して、位置(未来の状態)を描く

２．縦波

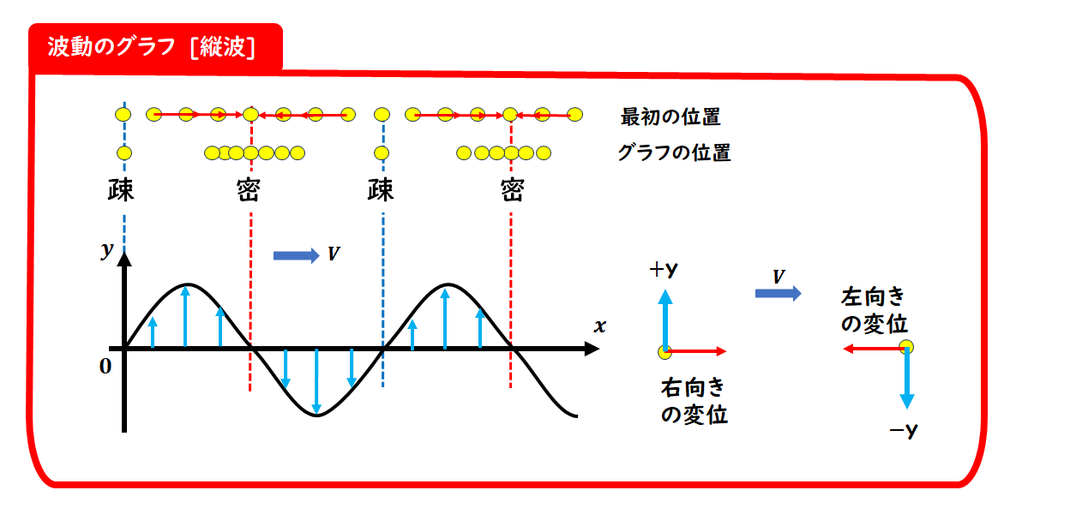
■ 波動には2種類の波がある

波動は、その変位の方向によって

以下の2種類に分類されます：

① 横波

変位の方向が、波の進行方向に垂直

例：弦の振動、電磁波など

グラフで表しやすく、

波動の学習では横波の表現が基本

② 縦波

変位の方向が、波の進行方向と同じ

例：音波

媒質の密度が高い／

低い部分（疎密）で表される

■ なぜ縦波も横波の形で表すのか？

縦波は本来、

媒質が進行方向に押し合い・引き合いながら進みます。
このままだとグラフにしづらく、

直感的に理解しにくいため、

以下のように扱います：

縦波の変位方向を“仮に y 軸方向”とみなして
横波のような形に変換してグラフで表します

こうすることで、

縦波も横波と同じ形式で

グラフに描けるようになります。

■ 進行方向が逆でも

グラフの形は変わらない？

進行方向が逆になっても、

変位は y 軸方向で表すため、

グラフの形自体は変わりません。
ただし、密な部分（圧縮）と

疎な部分（希薄）の位置関係は

進行方向に依存するため、
「疎密の分布」を正しく

判断する必要があります。

■ 音波に注意！

音波は典型的な縦波ですが、
問題によっては「縦波である」と

明示されていないことがあります。

そのため、

次のような設問では注意しましょう：

「疎な部分はどこか？」
「密な部分は？」
「このときの圧力変化は？」

→ 縦波の特徴（疎密）を意識しながら、解く必要があります。

✅ ポイントまとめ

波の分類：横波・縦波
縦波も「変位を y 軸として横波の形」で表す
グラフが同じでも、「進行方向の違い」による疎密の位置に注意
音波は典型的な縦波、疎密を問う問題に注意！

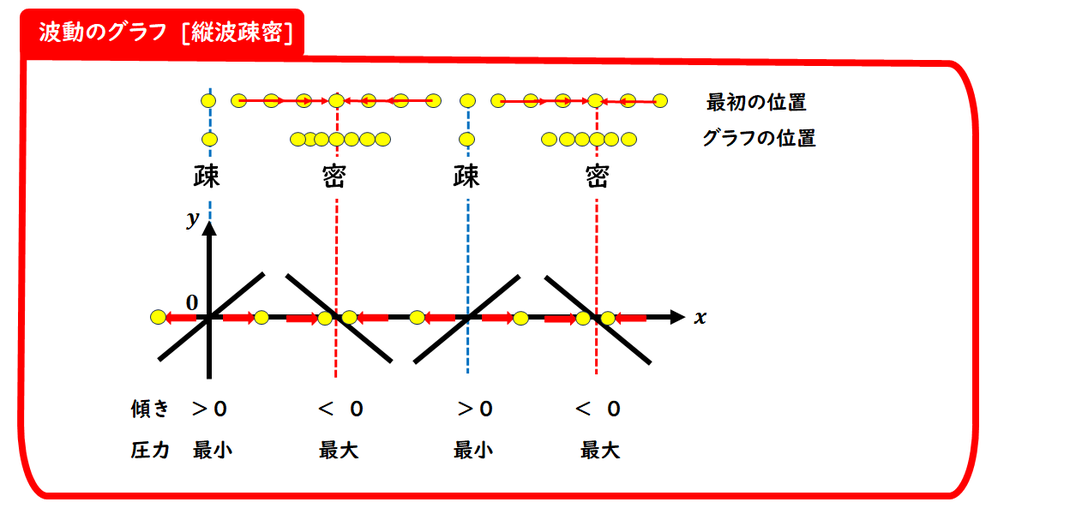
■ 縦波の問題でよく問われること

縦波（例：音波）に関する問題では、

「疎な部分」「密な部分」の位置を

問われることがよくあります。

■ 疎密を見分けるには？

縦波は、変位が進行方向と

同じ方向に発生する波です。
しかし、通常は変位を

「y軸方向（上下）」として表現するため、
実際の変位に“戻して”考える必要があります。

【手順のポイント】

・グラフ上の変位の傾きを確認する

傾きが正なら、右側の点は左へ動いている

その結果、密な（押し合っている）

部分ができる

このように、変位の傾きの方向が、

疎密の位置を決定します。

■ 圧力に関する出題にも注意！

まれに、縦波の圧力変化を

問う問題もあります。

密な部分（粒子が集まる） → 圧力が高い
疎な部分（粒子がまばら） → 圧力が低い

この関係は、感覚的にも自然なので、

ぜひ押さえておきましょう。

■ 疎密以外の問いは？

疎密や圧力に関する内容でなければ、
縦波の問題でも通常の

y–x グラフの問題と同じように考えてOKです。

たとえば、

波長 λ の読み取り
周期 T、振動数 f の計算
進行方向の把握

などは、横波の問題と変わりません。

✅ ポイントまとめ

縦波では「疎密の位置」が問われやすい
疎密の判断には「変位の傾きの向き」がカギ
密 → 圧力が高い／疎 → 圧力が低い（感覚どおり）
疎密に関係しない問いは、y–xグラフの通常問題として考える

問題：