エネルギー

仕事

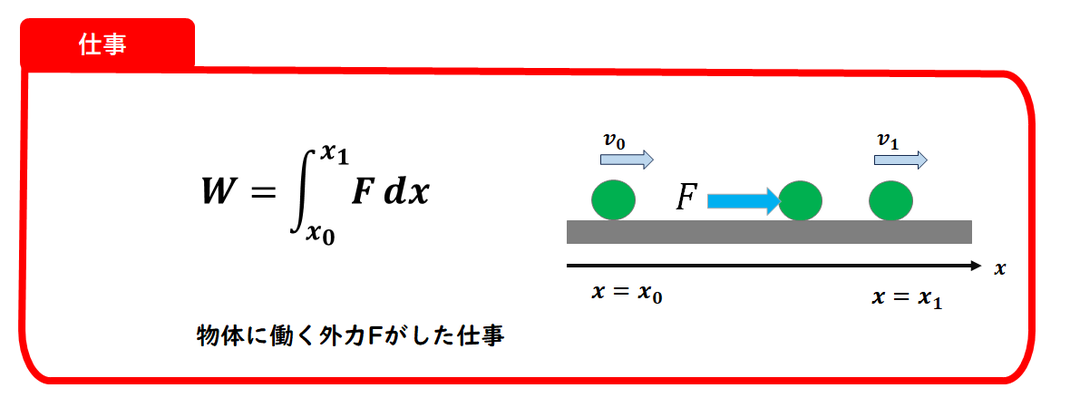
■仕事の定義について

仕事とは、物体がある経路を移動するときに、

力がその経路に沿ってする

エネルギーのやりとりのことです。

定義式は次の通りです：

仕事 = 経路に沿った距離 × 経路に沿った力

これは積分の考え方に基づくものであり、
力 $F$ が一定でない場合は、

グラフの面積などを使って求める必要があります。

注意点：

　経路と逆向きの力が作用する場合、

　仕事は負になります。

したがって、

外力の向きを正確に判断する

ことが重要です。

経路に沿った力とは、

力ベクトルを

軌道方向に射影した量であり、
これはベクトルの内積として表されます。

仕事とエネルギー

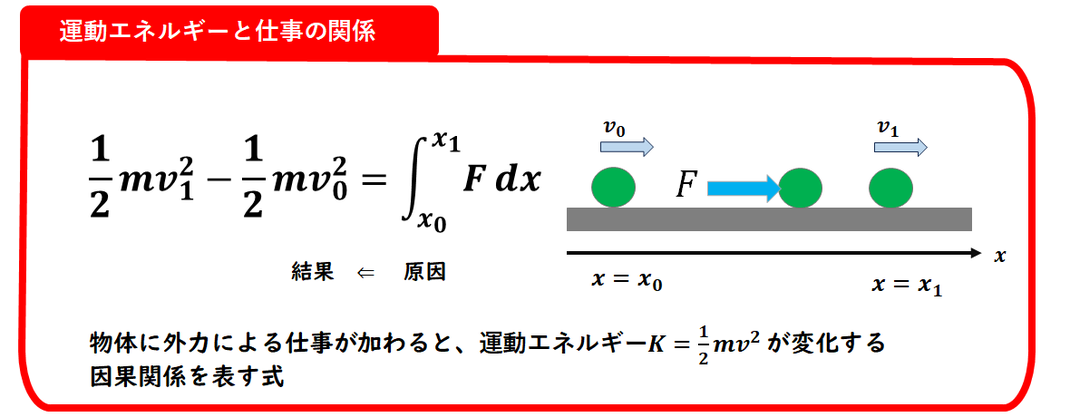
■運動エネルギーと仕事の関係

物体に仕事が加えられると、

その物体の運動エネルギーが変化します。

これは、

運動エネルギーと仕事の関係を

表す重要な式であり、
物理的な因果関係（原因と結果)

を示しています。

運動方程式と同様に、

「何によって運動が変化したか」を

考えるときに使われます。

ここで登場した

運動エネルギーという量について、
この式がどのように

成り立つのかを

確認しておくことが大切です。

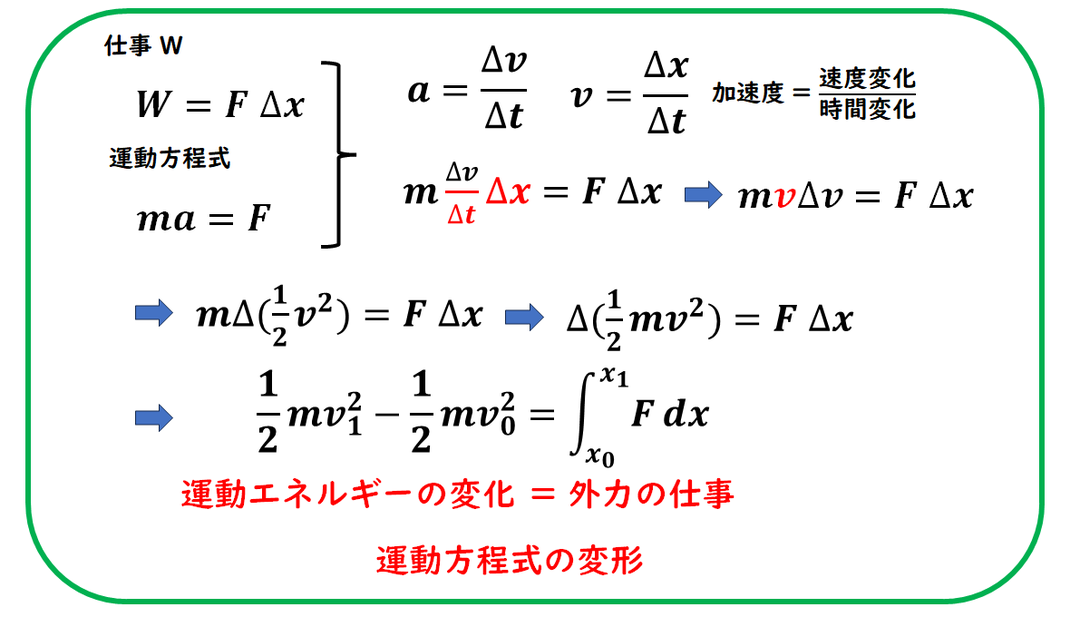
■運動エネルギーと仕事の関係（成り立ち）

運動エネルギーの式の

成り立ちは簡単ではありませんが、

「運動量を速度 $v$ で積分したもの」

と捉えることができます。

したがって、
運動エネルギーと仕事の関係は、
運動方程式を変形することで

導かれるものです。

この関係を利用するときには、

次の点が重要になります：

外力が何かを特定する（外力の検出）
外力の向きを正確に把握する
外力が加わる経路（移動距離や方向）を考慮する

式の左辺にある

運動エネルギーの変化は、
運動エネルギーが常に正の値を取るため、

次のように表せば十分です：

運動エネルギーの変化 =

（運動後）−（運動前）

エネルギーが増えれば正、

減れば負になるので、
この引き算の形で問題ありません。

エネルギーの問題は、

基本的には仕事の計算だけで

解くことができます。

しかし、

経路が複雑な場合や、

力が一定でない場合には、

仕事の計算が難しくなる(解けない時もある)

ことがあります。

そのため、
力学的エネルギー保存則を

活用することも非常に重要です。

力学的エネルギー保存則

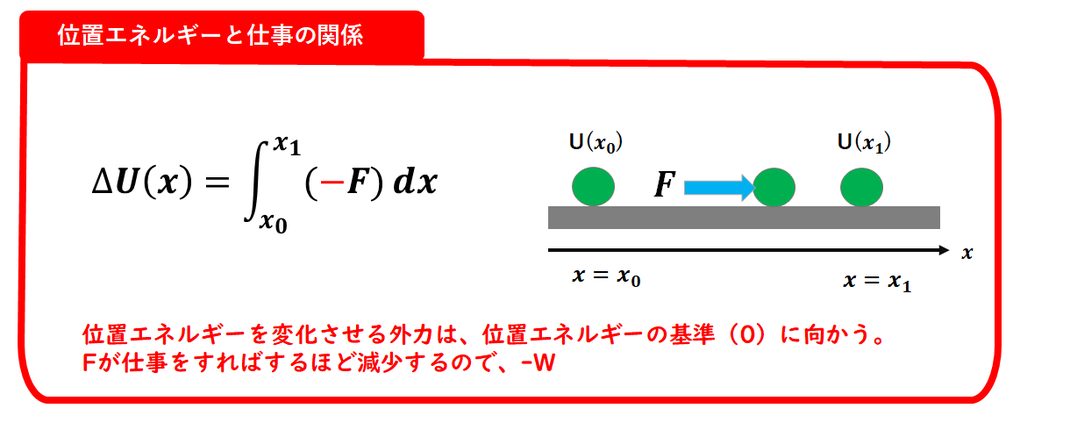
まずは、
位置エネルギーと仕事の関係

について見ていきましょう。

式だけでは分かりにくい部分もあるので、
例として「重力」による場合を

考えてみましょう。

重力による位置エネルギー：

U = mgh

重力によって仕事がなされると、

物体の高さはどうなるでしょうか？

そうです、高さは低くなりますね。

つまり、
位置エネルギーは減少する

ことになります。

仕事をすればするほど、

位置エネルギーは減少します。
したがって、

重力による仕事は

「–W」となります。

補足すると、

「位置エネルギーの変化 = −（重力がした仕事）」

という関係は、

保存力（重力など）による仕事は、

位置エネルギーの減少として現れる

という原理に基づいています。

位置エネルギーに関係する力には、

以下のような保存力があります。

重力
弾性力（ばねの力）
万有引力
クーロン力（電気力）

これらはすべて保存力と呼ばれ、

位置エネルギーを定義できる力です。

■力学的エネルギー保存則について

運動エネルギーの変化は、

位置エネルギーの変化と密接に関係しています。

位置エネルギーと仕事の関係に基づいて、

「運動エネルギーの変化＝

–(マイナス)位置エネルギーの変化」

という関係が成り立ちます。

このことから、

運動エネルギー＋位置エネルギー＝

一定（＝力学的エネルギーの保存）

となり、

力学的エネルギー保存則が成立します。

この保存則を使うためには、
外力が位置エネルギーに関係する保存力

（重力、ばねの弾性力、万有引力など）で

あることが必要です。

しかし、
外力が存在していても、

その仕事がゼロになる場合には、
力学的エネルギー保存則を

利用できることがあります。

これは、しばしば

暗黙の了解として扱われるため、
解答を見て「なぜ使えるの？」と

疑問に思った経験がある方も

多いのではないでしょうか。

「なぜ物体Aだけでなく、
急に物体Bまで含めて

力学的エネルギー保存則を

使うんだろう？」
…と思ったことはありませんか？

このような点については、
教科書や解答で

明記されていないことが多いです。

そのため、
「知らずに物体を限定してしまい、

力学的エネルギー保存則が使えなかった（間違えた）」
という経験がある方も多いのではないでしょうか。

さらに具体例として、

　・外力が常に物体の移動方向と垂直な場合

　（例：張力や法線力）

・動きが限定され、力が仕事をしない状況

　　（例：斜面上の物体に対する垂直抗力）

力学的エネルギー保存則は、
対象とする「物体系」全体に注目して

使うことが大切です。

外部からのエネルギーの出入りがないなら、

複数の物体をまとめて考えるのが自然です。

エネルギーや仕事に関する問題は、
基本的に
「運動エネルギーの変化＝仕事」
の式で解くことができます。

しかし、仕事を求める際に、
円運動などのように

経路が複雑な場合には、
移動距離を正確に

計算するのが難しいこともあります。

そのような場合は、
経路に依存しない
力学的エネルギー保存則を

利用すると、
より簡単に解けることがあります。

力学的エネルギー保存則は、

「保存力（重力や弾性力など）」

だけが働いているとき、
運動エネルギーと位置エネルギーの

合計が一定になるという法則です。
経路に関係なく

始点と終点のエネルギー差だけで

解けるため、非常に便利です。

エネルギーに関する問題では、
運動量保存則と併用することが多いため、

エネルギーの演習を終えた後は、
運動量保存則や力積の演習も
あわせて行うようにしてください。