ばね 弾性力
位置エネルギー
1.ばねの力 弾性力
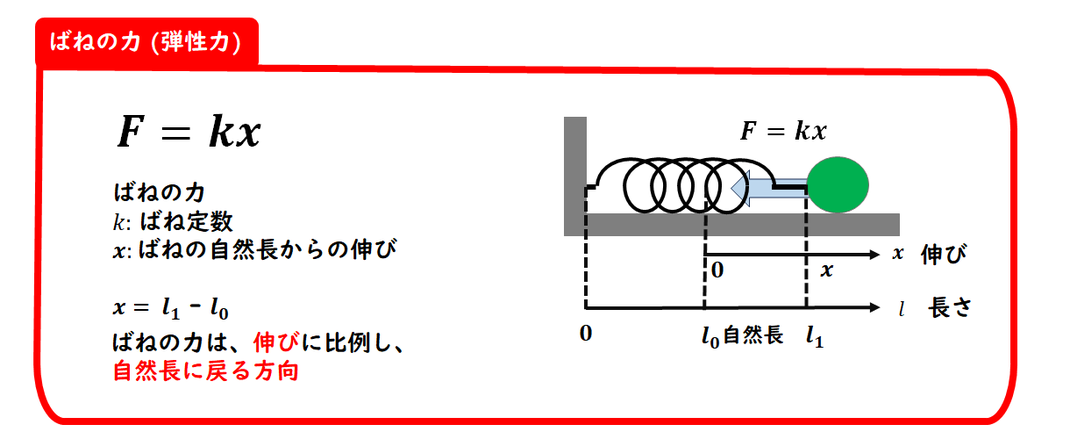
ばねの力(弾性力)は、
ばねの伸びに比例します。
このときの比例定数を
「ばね定数」と呼びます。
ばねの力の大きさは、
あくまで
「自然長からの伸びまたは縮みの量」
に比例し、ばねの全体の長さそのもの
には関係ありません。
また、ばねの力の向きは、
常に自然長へ戻ろうとする方向です。
したがって、
ばねを縮めている場合には、
力は+x方向を向きます。
2.ばねの力の位置エネルギー
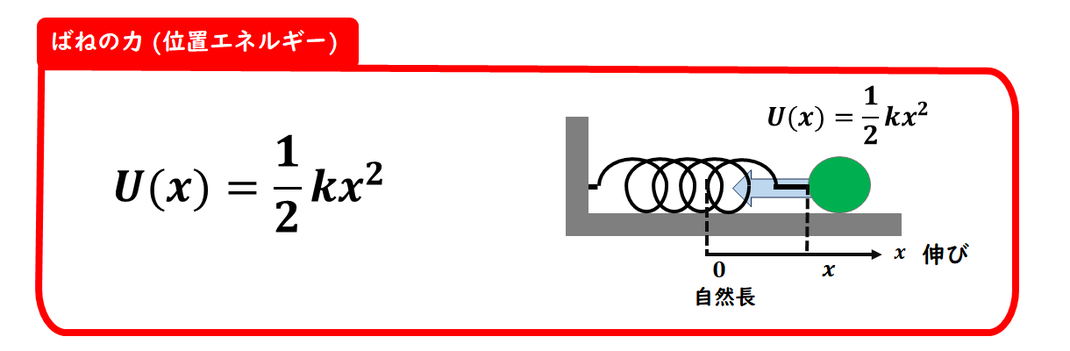
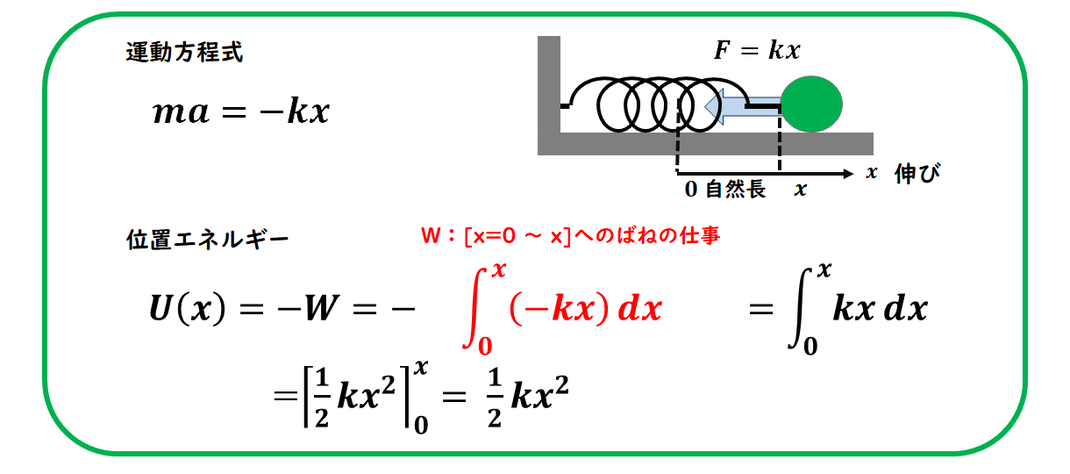
ばねの力には、
位置エネルギーが存在します。
この位置エネルギーは、
ばねの力による仕事と
位置エネルギーの関係
(U = -W)から導かれます。
計算によって
導出することも可能ですが、
公式として記憶して
おくべき重要な式です。
2.合成ばね定数
直列
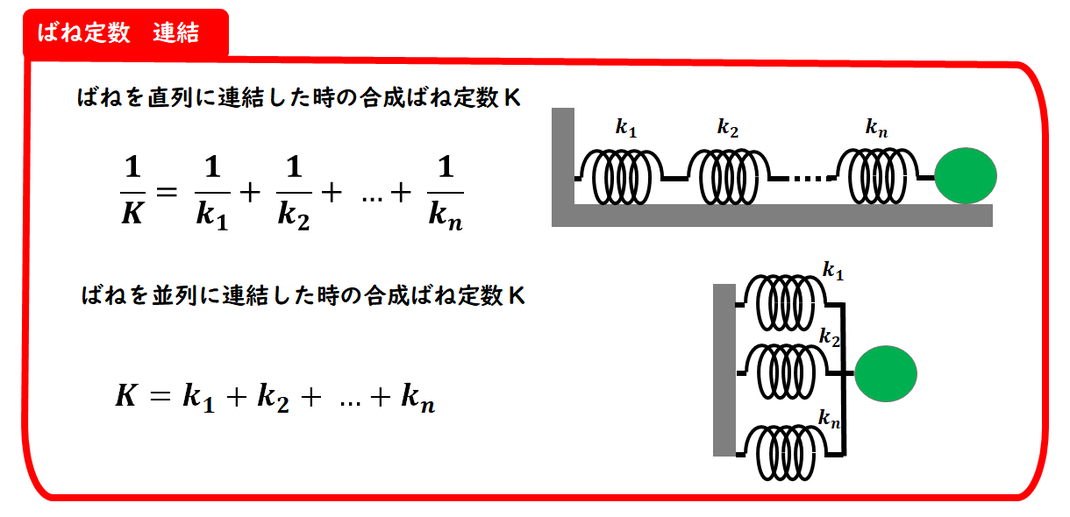
ばねを連結した場合の
合成ばね定数についてです。
感覚と逆の結果になることがあるため、
注意が必要です。
この合成ばね定数は、
そのまま利用する場合もありますが、
単振動の問題などでは、
合成ではなく分割して扱うこともあります。
したがって、
公式だけでなく、
導き方を理解しておくことが重要です。
以下に、
その導き方を示しますので、
公式と合わせて覚えましょう。
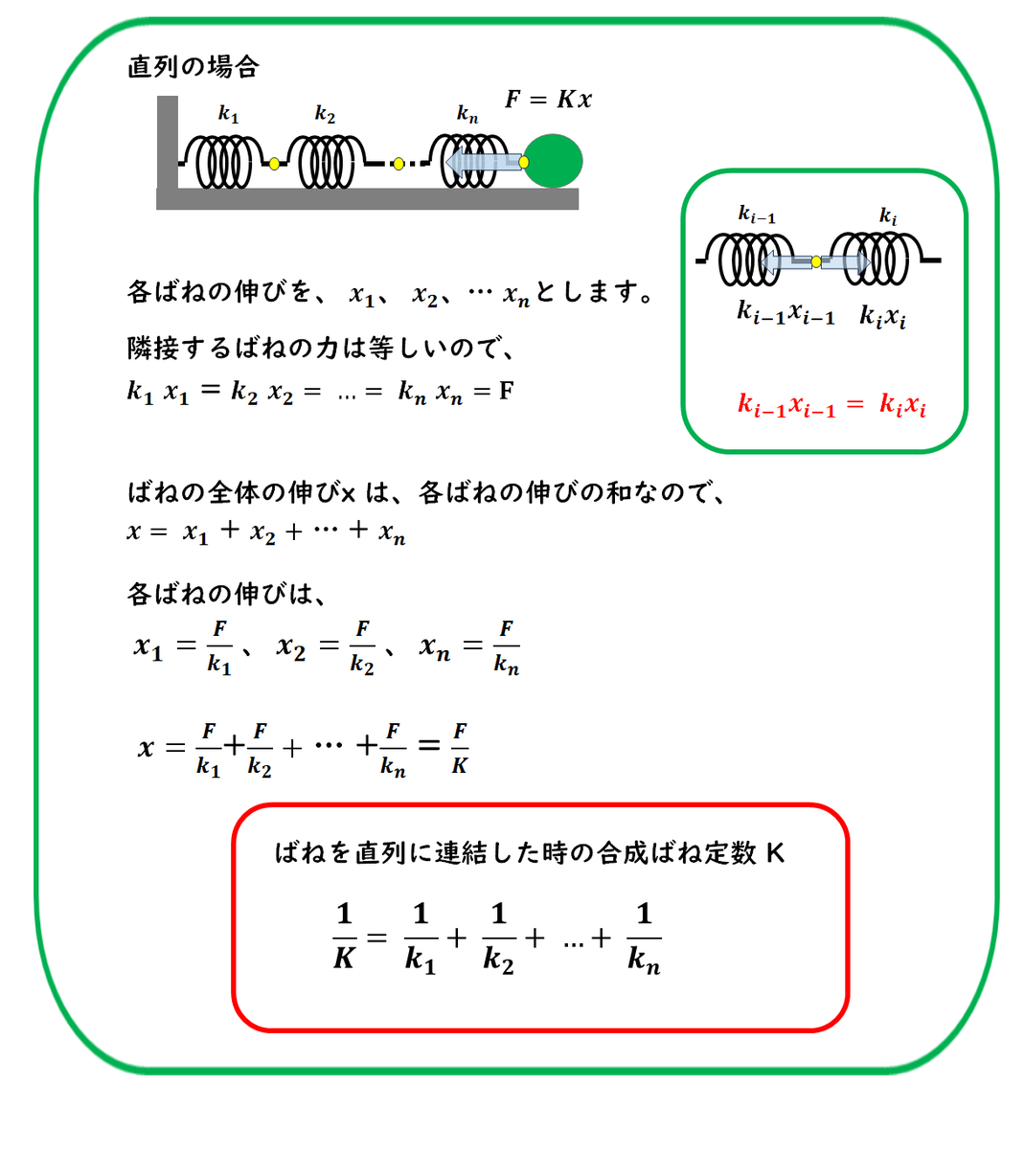
直列につないだばねの場合、
隣り合うばねには
同じ力がかかります。
それぞれのばねの伸び
(変位)は異なりますが、
ばね全体の伸びは、
各ばねの伸びの合計になります。
この関係から、
直列における合成ばね定数を
導くことができます。
並列

並列につないだばねの場合、
各ばねの伸びは等しくなります。
したがって、
ばねの力はそれぞれのばねで発生し、
その合計が全体の力になるため、
合成ばね定数は和で
求めることができます。
直列と並列の式が
混ざって混乱したときは、
まず並列の方を
思い出すとよいでしょう。
また、
コンデンサの合成と
似ていると考えるのも一つの覚え方です。
分割
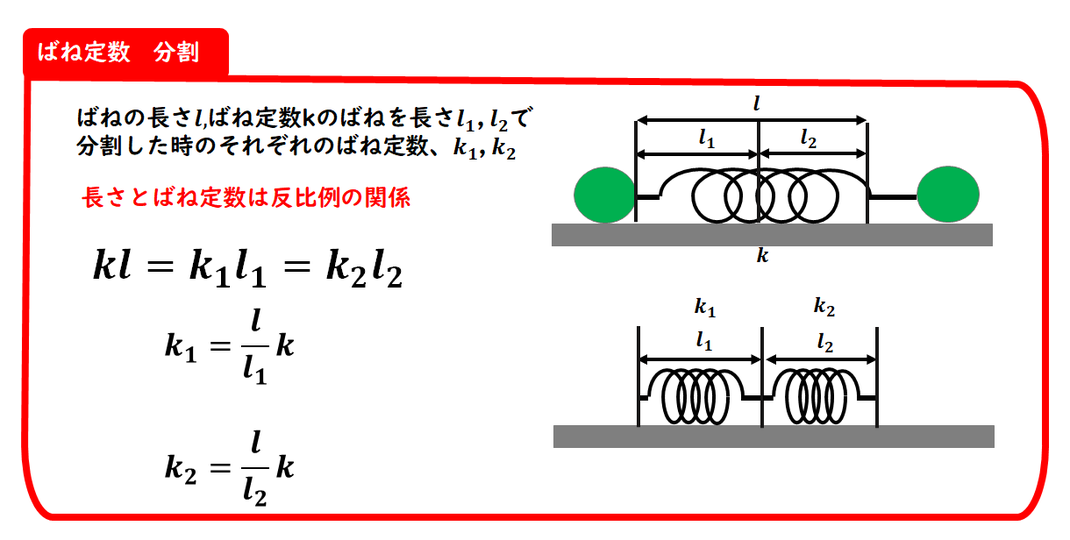

ばねを分割したときのばね定数
について説明します。
ばね定数は、
ばねの長さに反比例します。
たとえば、
ばね定数k のばねを
2つに分けた場合、
1本あたりのばね定数は 2k になります。
逆に、ばねk を2個直列につなげると、
合成ばね定数は 1/2k
になるため、
長さとばね定数は反比例の関係に
あると覚えておくと便利です。
この分割の考え方は、
単振動の問題でよく利用されるので、
しっかり理解しておきましょう。
