必須問題は、a、b（斜面方向）、c、g です。
その他の問題は標準問題となります。

必須問題で間違えた場合は、
解説をよく読み、

教科書や参考書なども活用して、

もう一度解き直してみてください。

 すべての問題が正解だった場合は、

「力の検出」は合格レベルです。

自信を持って次に進みましょう！

何問くらい正解できていたでしょうか？
今回は計算を必要としない問題なので、

計算ミスはありません。

ただし、力の分解において

sin や cos を取り違えたというミスは、
意外と多かったのではないでしょうか？

❗ 間違いの傾向として、以下の点がよく見られます：

   ・力の分解のミス
　     → sin と cos の使い分けや、

             分解方向の設定に注意が必要です。
　・物体Bに働く力の見落とし
　　→ 反作用の力 や 重力の作用点 を

　　　見逃すケースが多いです。
　・摩擦力の向きの誤認
　　→ 摩擦力は物体の動きに逆らう向きに

　　　なることを意識しましょう。
　　　静止摩擦力は特に向きを取り違えやすいです。
　・張力の描き方・方向の誤り

物理の問題は、
正解・不正解の理由が明確に存在します。

そのため、

不正解だった場合は、なぜ間違えたのかを

しっかり考えることがとても重要です。

単に答えを見るのではなく、
どの考え方が誤っていたのか、

どの力を見落としたのか、

何を勘違いしていたのか
といった

不正解の原因を明確にすることが、

次の正解につながります。

今回の問題では、

3種類の力が登場しました。

力の検出において、

外力の種類や大きさがはっきりしない場合には、
力の検出方法（見つけ方）を

しっかり身につけることが大切です。

力学で扱う力の種類は、多くても10種類程度です。
それぞれの力がどのような状況で働くか、

どのように見つけるかを学んでおきましょう。

今回の問題で間違えた箇所があれば、
力の検出方法を確認したうえで、

もう一度その問題を解き直してみてください。

a.

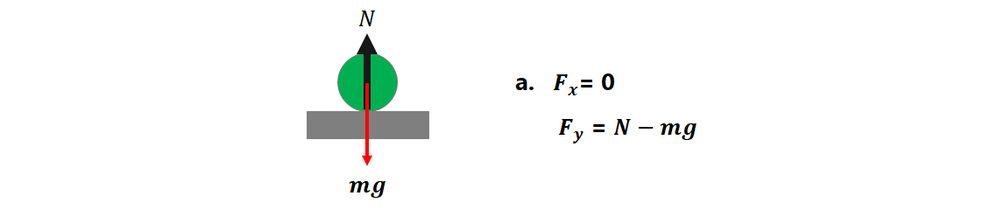
物体の周りをなぞると床があります。　

働く力は、接触力 ：床からの抗力 

重力 です。

合力はｙ方向になります。

b.

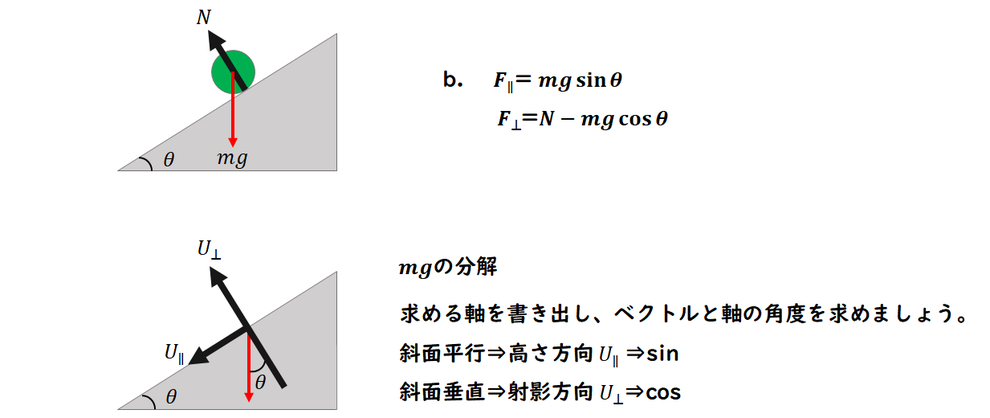
力の検出は、a.と同じです。　

働く力は、接触力 ： 床からの抗力　

重力になります。

抗力は斜面垂直方向です。

合力の指示が斜面平行、垂直です。

抗力 は斜面垂直方向です。

重力は指示方向とあっていません。　

重力を分解する必要があります。

分解する軸を書き、

分解する軸と重力の間の角度を求めます。

角度と軸からcos、sinが決まります。

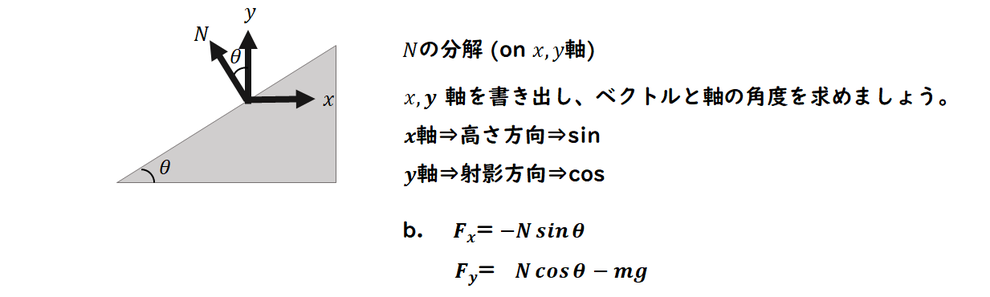
後半は、

斜面ではなく、x軸 、y軸の合力です。　

重力はｙ軸 方向です。

抗力Nをx、y軸 へ分解します。

分解する軸と力の角度を求めて、

sin、cosをきめましょう。

cos・sin の間違いはありませんか？

cos と sin の取り違えは、

よくあるミスです。

実際、私自身も間違えることがあります。

ですが、

これらは問題の序盤、

つまり間違えると、

その後の設問すべてが

誤りになってしまう可能性があります。

この問題では、角度を 0° として考えると、
斜面方向・x方向・y方向のいずれにおいても

a. の状況と一致します。

a. の解答はすぐにわかるはずです。
重要な場面では、

解答後に cos・sin の再確認する

習慣を持ちましょう。

c.

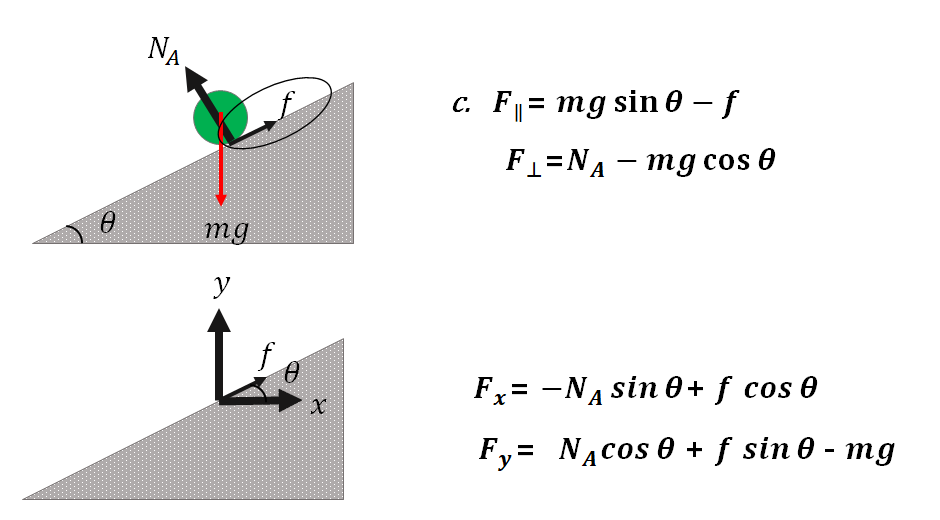
b.と似ていますが、

傾斜が荒く摩擦力があります。

摩擦力の向きが問題となります。　

摩擦力以外を考えると、

斜面方向には重力が働くので、

下に落ちることになります。　

基本的に摩擦力は動きを妨げる方向になり、

斜面上側になります。

斜面平行、垂直の力の合力は、 

b.の復習です。　

摩擦力の向きが傾斜平行なので

摩擦力を追加します。

ｘ軸、ｙ軸の合力は、摩擦力を分解します。　

摩擦力 の方向は、斜面の角度と同じなので、

x軸⇒射影方向⇒cos 　

ｙ軸⇒高さ方向⇒sin 

となります。

b.の復習 と、分解した摩擦力を加えます。

A が上側に動いていると考えた人へ

摩擦力が

斜面下向きになっていたとしても、
A が上に動いていると

仮定したのであれば、

それは正解です。

ただし、通常の状況では、

物体が自然に上に動くことは少なく、

やや不自然です。
そのような場合は、

説明があるはずです。

d.

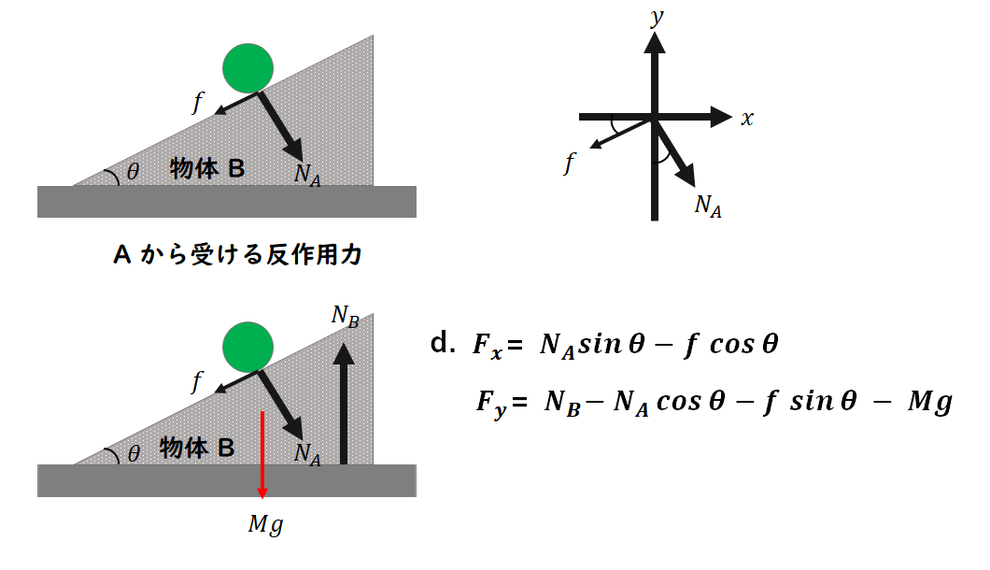
物体Bの働く力です。

物体Bの接触はAと床になります。

Aからの接触力を考えます。　

物体BがAから受ける力は

Aの抗力の反作用になるので、

Aからの接触力は、

Aの抗力と大きさは同じで

向きが逆向きの力になります。

床からの接触力は、垂直抗力

床はなめらかなので摩擦はありません。　

最後に、物体 Bに加わる重力Mgです。

物体 B働く力は、4つの力になります。　

複雑ですが、

力の探し方で、探すことができます。

間違えの例としては

Aからの反作用としての垂直抗力と、

床からの垂直抗力が、

大きさが同じと解答している方は

間違えです。　

区別しましょう。

物体Bの重力も、A分を加味して(m+M)g

としている場合も間違えです。

物体 Ｂにかかる重力は  Mgです。

あとは、

x軸、ｙ軸に分解して合力を求めます。　

軸と力の角度を丁寧に求めましょう。

台（物体B ）の運動を求める問題は、

台が、x方向に動くことになるので、

ｘ軸、ｙ軸の合力が必要になります。　

傾斜の問題は台が動くと

ｘ軸、ｙ軸の分解が必要になります。

e.

e、f は似ていますが、
少しわかりにくく、差がつきやすい問題です。
確実に正解できるようにしておきましょう。

e. のポイントは、「台に力を加える」場合です。
たとえば、

ノートの上にペンや消しゴムをのせて、

ノートを動かす状況を思い浮かべてください。
また、

電車の中の人と電車自体の動きを

イメージすると理解しやすくなります。

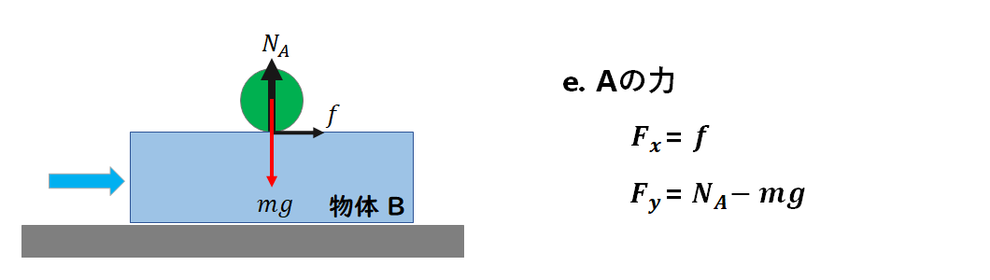
物体Aの力です。　

接触力はBからの接触力です。　

面が荒いので、垂直抗力と摩擦力です。

あと、重力です。

垂直抗力が y 軸方向に働くのは問題ありません。
問題は、摩擦力の向きの理解です。

多くの解説では、以下のように説明されています：

「B に力を加えて動かすので、

B の動きが基準になります。
B に対して摩擦力はその動きを妨げる向き、

つまり –x 方向に働きます。
その反作用として、

A には +x 方向の摩擦力が働くことになります。」

「わかりにくい」と感じる人も

いるかもしれません。

そこで、

A の運動について考えてみましょう。

電車の例を思い出してください。

動いている電車に乗っているとき、

電車が動き出すと、中の人（= A）は、

どちらに動こうとするでしょうか？

当然、

電車（= B）と同じ方向に動きます。

ということは、

A は電車（B）との接触によって、

進行方向に力を受けている

ということになります。
その力の正体が、

B から A に働く摩擦力（+x方向）です。

Ａの合力はすべて、x軸、y軸方向で、

分解する必要ありません。

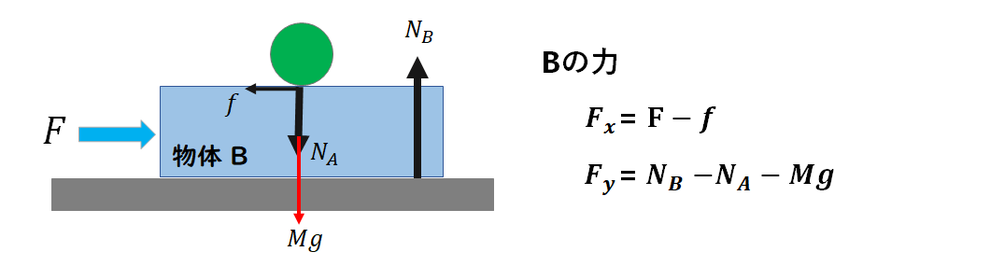
今度は物体Ｂです。

物体Ｂの接触力は、Ａと床、問題のFです。

Ａの接触力は、

反作用としての

垂直抗力、摩擦力（Aの時と同じ大きさ）

床からの接触力は、垂直抗力

そして重力　Mgです。　

あとは符号に注意して合力が求めます。

台を動かす問題では、

乗っている物体の摩擦力は、

台に働く力の向きと

基本的には同じで良いです。

f.

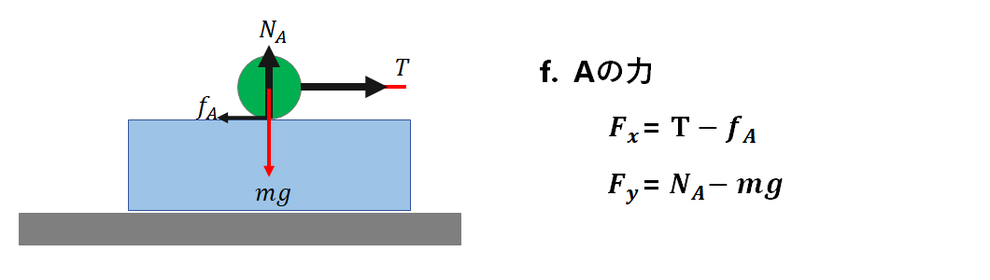
これは「A に力を加える」タイプの問題です。

まずは、物体 A の運動から

考えてみましょう。

よく考えてみると、
この問題は

床が限られた範囲に描かれているだけで、
実際には「床の上で物体を押す」という、
これまでに見てきた

a. や b. の問題と同じ構造です。

つまり、物体 A だけに注目すれば、

特別なことはありません。
a. や b. の問題と同じように考えれば良いのです。

接触力は、糸、物体Bからの接触力、

垂直抗力、摩擦力の３個です。

摩擦力は、－x方向です。　

あと、重力 mg です。

糸から受ける力の向きですが、

糸は外側の張力で引っ張られています。

その反作用が

物体Aが糸から受ける接触力になるので、

糸 の張力は、糸がある方向になります。　

糸に引っ張られているので、

直観的にAに働く張力の向きは

糸が引っ張る方向と

わかりますね。

働く力は、x軸、y軸に平行なので、

分解はありません。

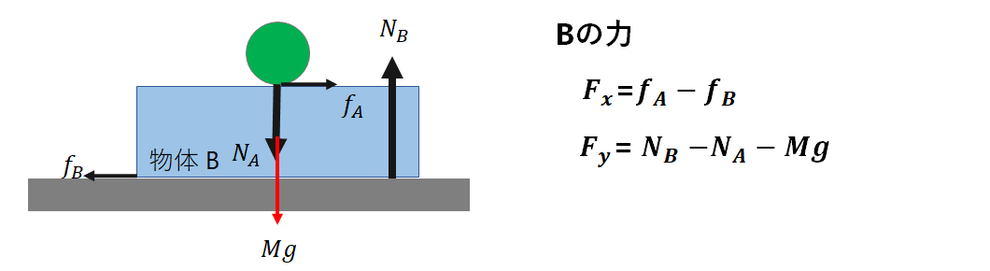
物体Bの場合です。　

接触力は、Aからの反作用、

床からの垂直抗力、摩擦力です。

床からの摩擦力の向きですが、

物体 Bは、

Aの摩擦力で+x方向に動くので、

その妨げとなる方向となる

床からの接触力の摩擦力は

－x方向です。　

感覚とあまり変わらないと思います。

床からの摩擦力が物体Bの外力とみなせば、

Aの摩擦力の向きと同じなってますね。　

e.と同じになってます。

あとは、物体 Bの合力は符号の向きに

注意して合力を求めましょう。

g.

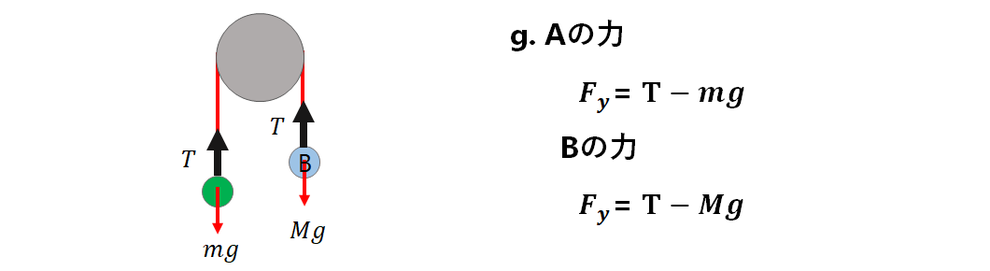
A、Bともに、接触力は糸です。　

糸の張力はどこでも同じなので、

どちらも大きさは同じくTです。

重力はそれぞれ、mg、Mgです。

ｙ方向の合力は分解なく

求めることができます。

h.

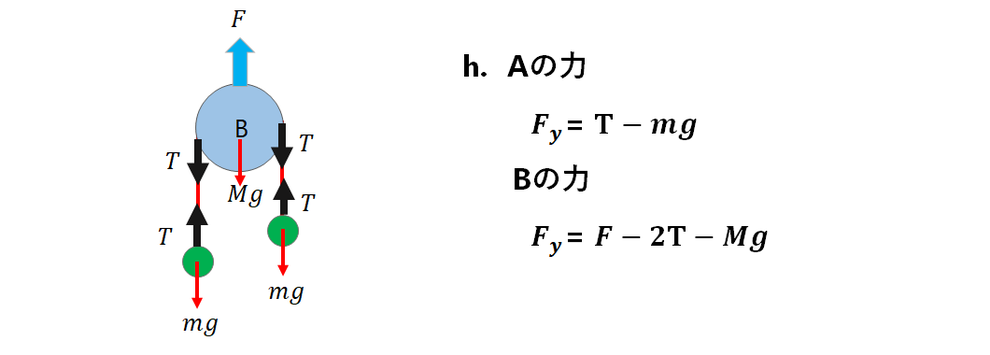
Aの合力は、g.と同じです。

Bの接触力は、問題のF、糸です。

Bは２か所、糸で引っ張られています。

糸の張力はどこでも同じなので、

糸の働く力は２Tです。

あとは、重力Mgです。

運動方程式へ