力学演習
運動方程式を解く
解説
必須問題:
c、d、i、j、m
基本問題:
b、e、g
応用・難問:
h、k
入試レベルでは、全問正解を目指しましょう。
特に必須・基本問題は落とさないことが大切です。
■摩擦力の問題は得点源に!
摩擦力の問題は、得意分野にしておきたい重要な単元です。
もし、摩擦力の向きや大きさで間違えてしまった場合は、
まずは摩擦力の仕組みをしっかり理解しましょう。
そのうえで、もう一度同じ問題を解いてみてください。
理解が深まると、間違いも自然と減っていきます。
誤答の原因に、
文字(記号)の計算ミスではないでしょうか?
これは、
慣れによる部分が大きいので、
焦らず繰り返し訓練していくことが大切です。
訓練を続ければ、必ずできるようになります。
もし、時間がかかりすぎると感じた場合は、
一度その問題から離れて、
次の内容に進むのも有効です。
学習には波があります。
粘り強く続けていきましょう。
全問正解できた方は、
次のステップとして
「拘束条件」の問題に進みましょう。
より複雑な運動の理解が深まり、
応用問題にも強くなっていきます。
d.
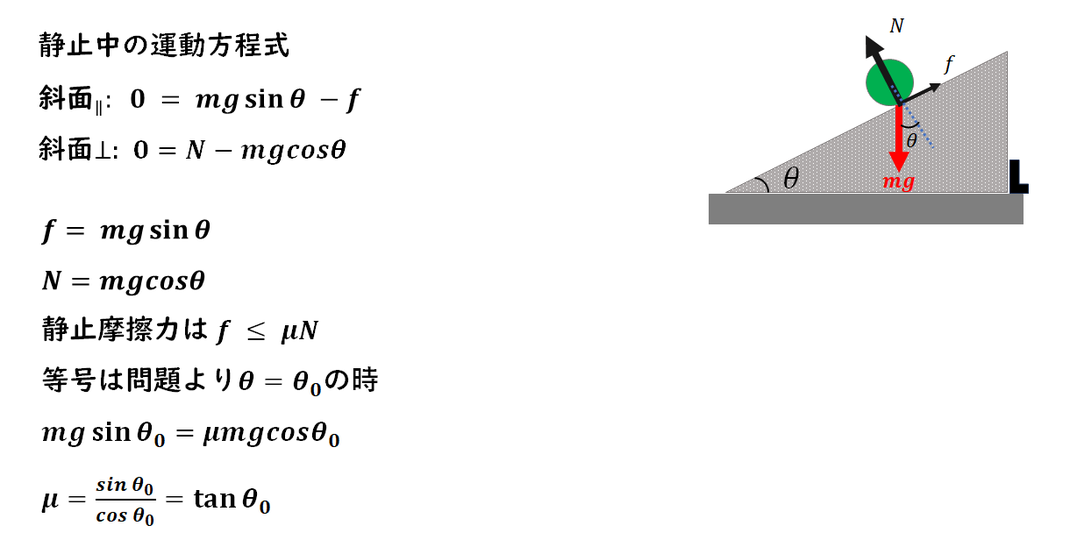
1.斜面方向の運動方程式を立てます。
斜面上の物体に働く力を分解し、
斜面に沿った方向で運動方程式を作成します。
2.摩擦力の式を用います。
物体が静止している場合、
摩擦力は外力につり合う値となります
(最大ではない可能性もあります)。
3.滑り出す直前の状態では、
摩擦力が最大静止摩擦力に達しているため、
このときの条件をもとに等号(=)を
用いて方程式を立てます。
4.等式の運動方程式を解くことで、
最大摩擦係数を求めることができます。
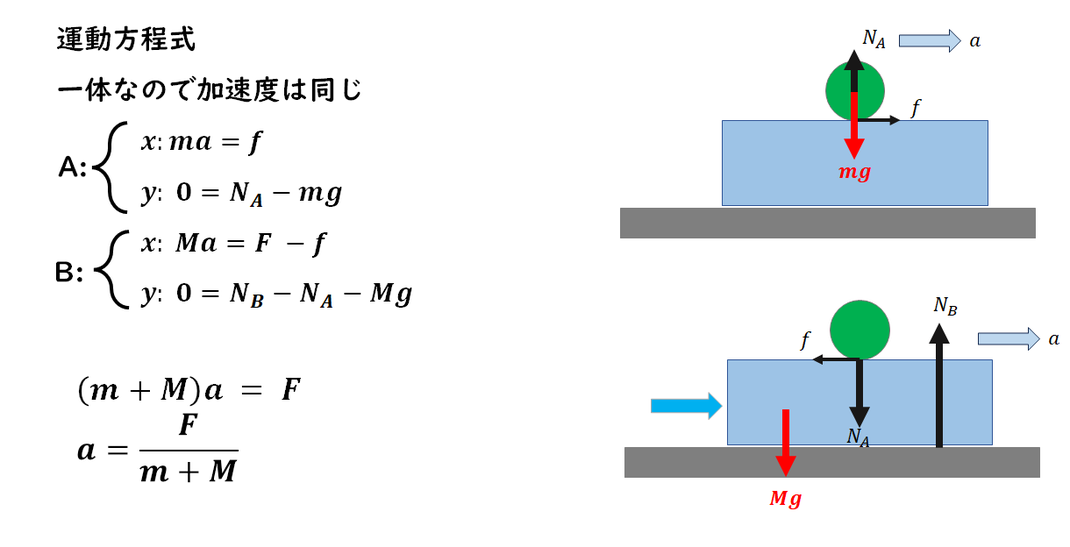
g.
A、B に働く外力を調べ、
それぞれの運動方程式を立てます。
今回は一体運動のため、
A、B は同じ加速度a を持つとします。
次に、
作用・反作用の関係にある
摩擦力を打ち消すために、
両式を加えます。
この操作によって摩擦力が消去され、
加速度a が得られます。
2)
Aが滑らない条件は、
Aの摩擦力が静止摩擦力の
ことなので、
静止摩擦力の条件を求めます。
ここからFの式に変形して解答します。
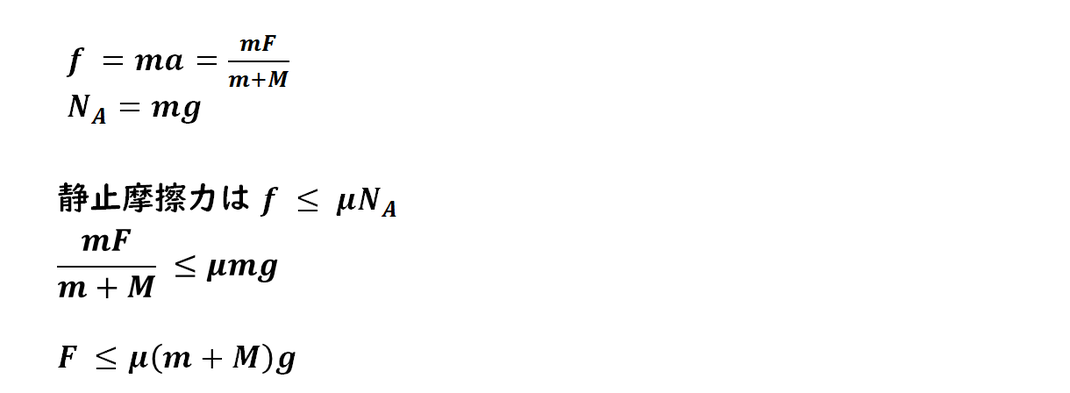
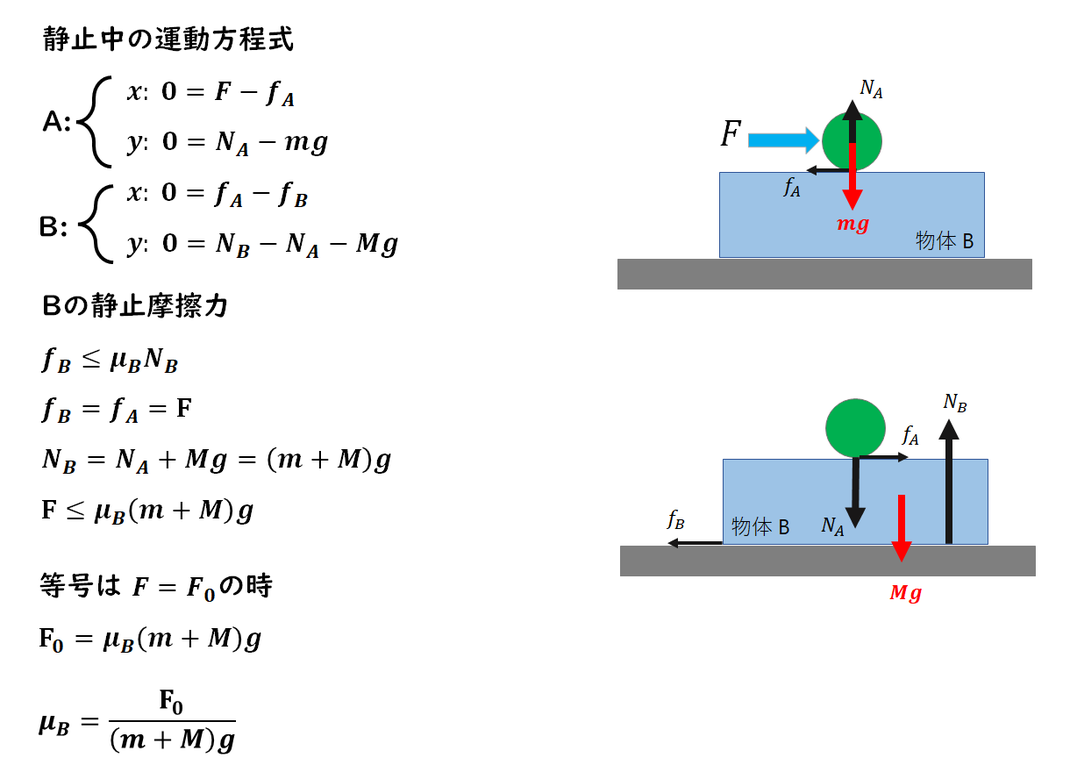
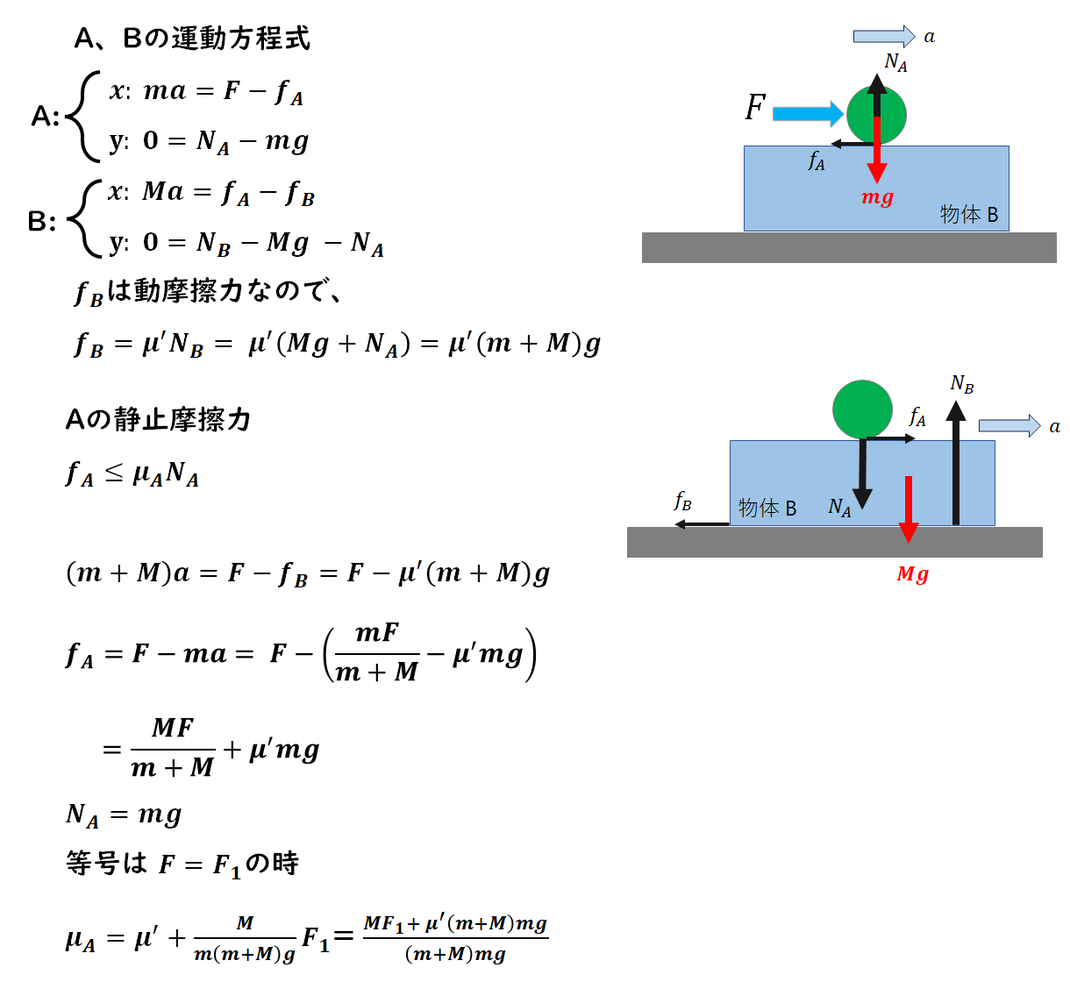
h.
1)
F = F0で一体となって動きます。
静止中の運動方程式を求めます。
床とfBの静止力を求めます。
F = F0が等号条件なので、
代入して静止摩擦係数を解答します。
2)
一体で動くときの運動方程式を求めます。
fAの静止摩擦力を求めて、
F = F1の時が等号条件になります。
静止摩擦係数を解答します。
K.
1)
静止摩擦力を求め、
等号条件M =M0より
M0を求めます。
まずは、
静止時の運動方程式を求めます。
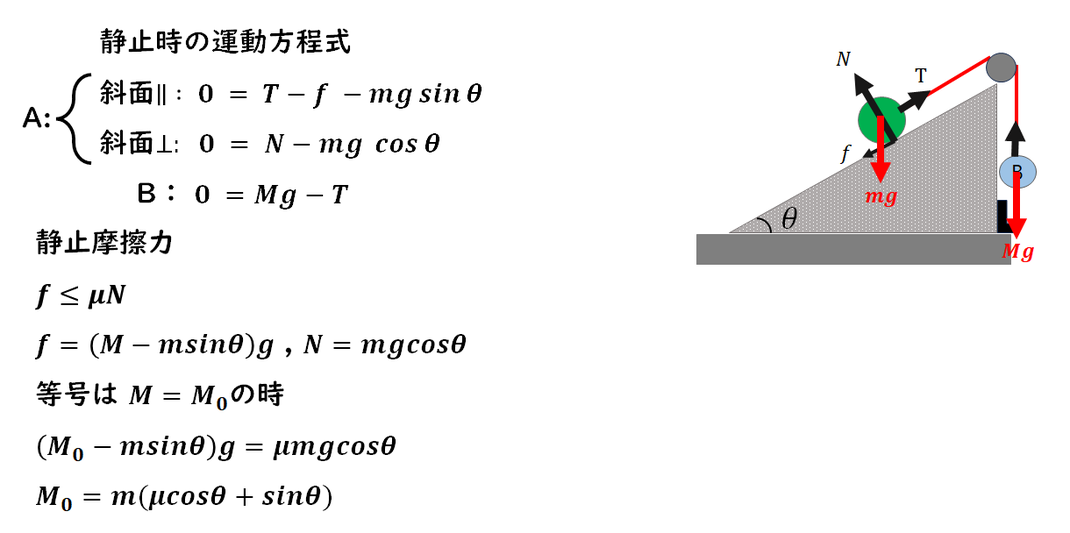
静止摩擦力fを求めます。
求まる時は、作用反作用となる
Tを消す式の和を行えば、
fが求まります。
等号条件からM0を解答します。
2)
運動方程式を求めます。
Aは、運動しているので、
摩擦力は動摩擦力に変わり、
求まることができます。
この場合も、
作用反作用になるTを
消す式の和を行い、
加速度を求め解答します。

摩擦力の問題では、
静止摩擦力と動摩擦力を正しく区別し、
それぞれの場合で
運動方程式をきちんと分けて立てる
ことが重要です。
また、
運動方程式を立てる際には、
摩擦係数μ を直接代入せず、
まずは式の形として整理することを
徹底しましょう。
このような基本を守ることで、
ほとんどの摩擦の問題に対応できます。
さらに、
他のパターンの問題にも挑戦し、
実践を重ねて理解を深めましょう。
in the processing of making a website.
Sorry...
