運動量

１．力積と運動量

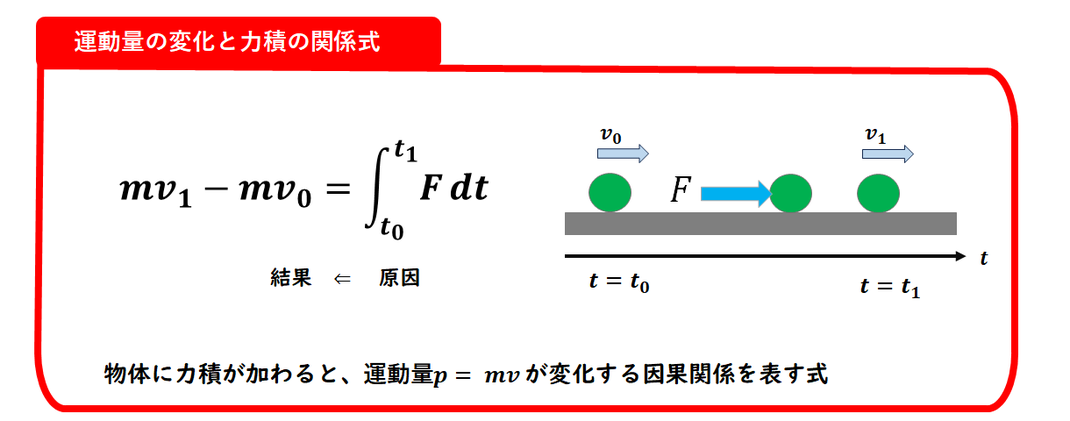
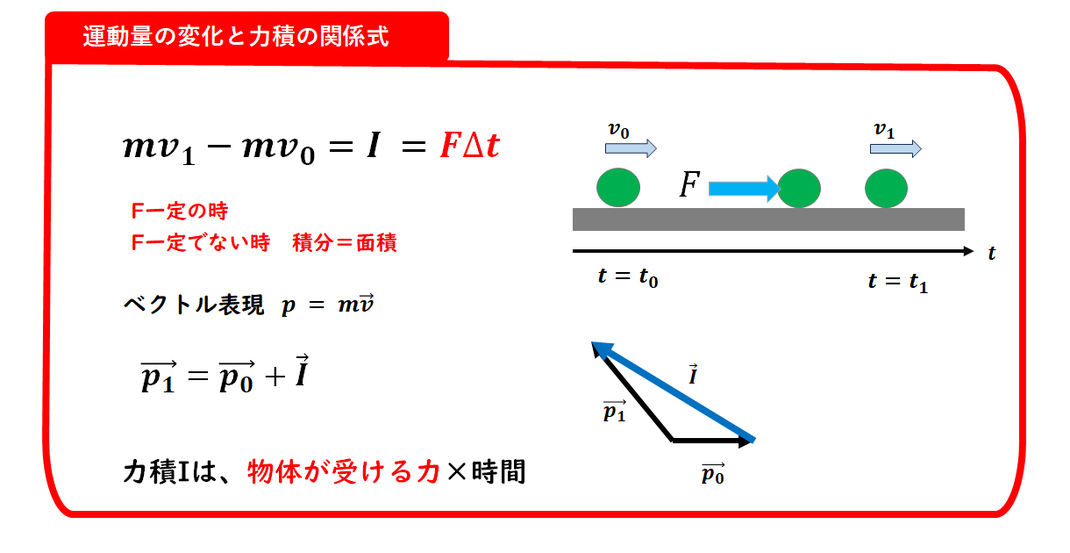
力積と運動量の関係式です。
教科書では、

力積を積分で表し、

その結果を $I$ としていることが多いです。
しかし、

積分が苦手な人にとっては、

少しわかりづらいかもしれません。
そんなときは、

この式がどのように導かれたのかを考えてみましょう。

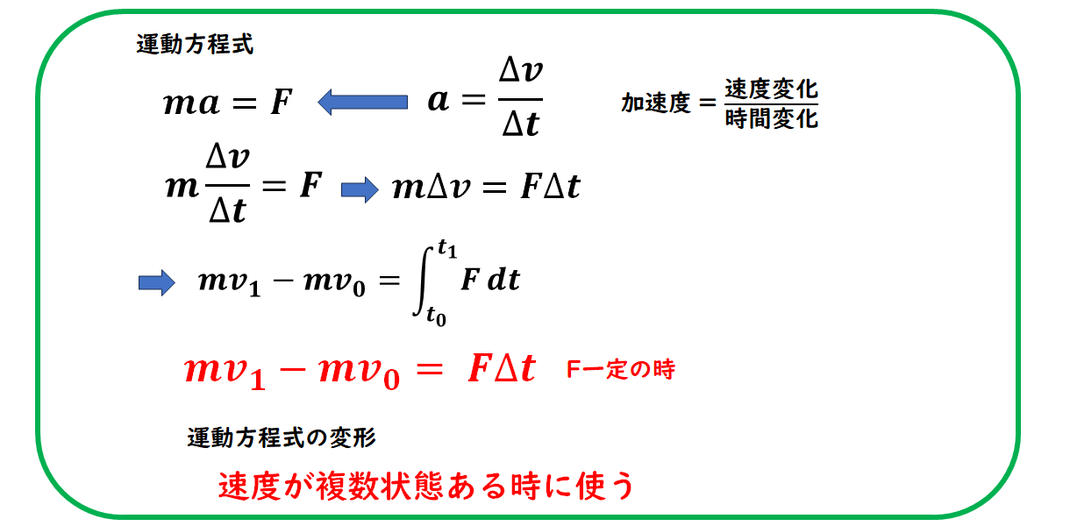
運動方程式を変形することで、

力積の式が導かれます。
つまり、

力積の式は

運動方程式の別の表現だと

考えることができます。

力積の式を立てるということは、

運動方程式を使っているということです。

このとき、

「どの力が働いているか」を

しっかり意識することが大切です。

また、

力積も物体に加わる「外力」の結果

であるという点を忘れないようにしましょう。
問題を解く際には、

力の「切り分け（どの力を使うか）」

も重要になります。

・ある瞬間の運動を表現したい場合

→　運動方程式を使います。

　（例：加速度や力が分かっているとき）

・ある時間の前後で速度の変化を扱いたい場合

→　力積-運動量関係式 または 運動量保存則 を使います。

　（例：衝突や、力が加わる時間が短い場合）

積分とは、

ある量を時間などにわたって

集積することを意味します。

運動方程式

この運動方程式を

ある時間区間にわたって積分すると、

運動量の変化 = 力積(積分)

という関係式が得られます。

したがって、

「運動量の変化＝力積」を、

運動方程式とは

別のものとして考えてはいけません。
両者は本質的に同じ運動の記述であり、

状況や目的によって使い分けるだけです。

前後の運動を表現するためには、

ベクトルを使う必要があります。

運動量や力積は

向きのある量（ベクトル）なので、
運動の前後の変化を正しく捉えるには、

ベクトルとして扱う必要があります。

たとえば、速度が反転する場合など、

符号（方向）が重要になるため、

スカラー（大きさだけの量）で

処理してしまうと誤りに繋がります。

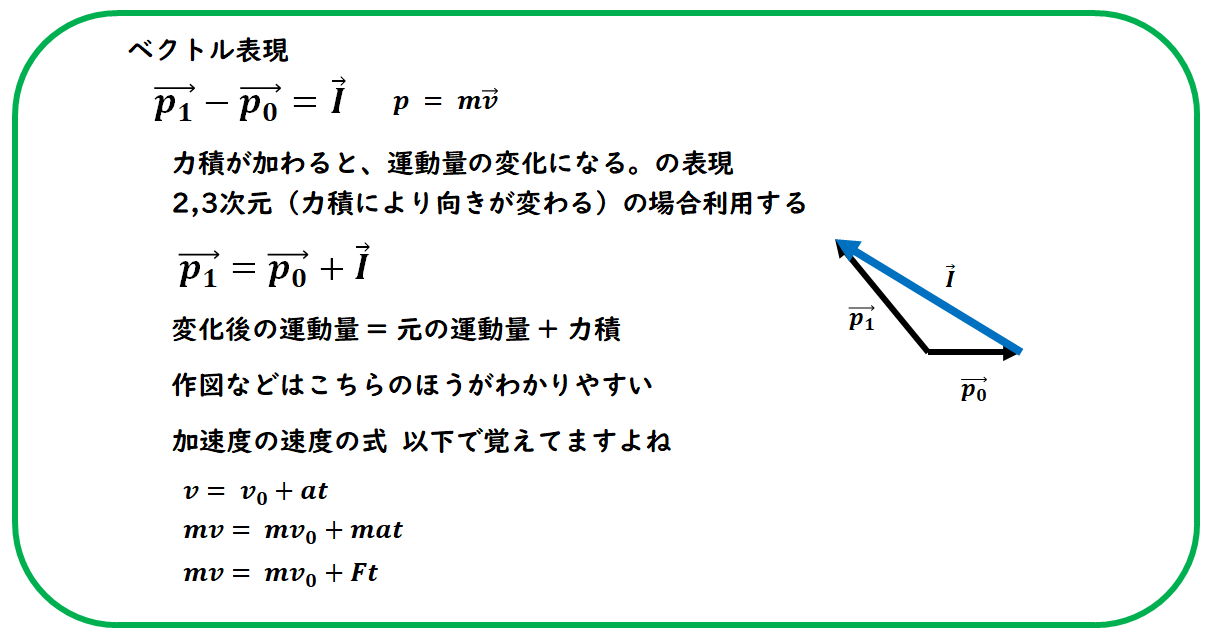
覚え方は、

自分にとって覚えやすい方法で構いません。

ただし、

ベクトルの引き算は間違えやすいため、
和の形で図を描いて考える方法

がおすすめです。

方向の取り違えを

防ぐのに役立ちます。

問題が解けるように

まとめると

力積だけを扱う問題は多くありませんが、

運動量保存則の基礎となる概念なので

非常に重要です。

また、

熱力学や音、光などの分野では、

力を直接求めにくい場合に、

力積の考え方が有効になることがあります。

したがって、

力積の意味や使い方を

しっかり理解しておくことが大切です。

問題を解いてみましょう。

力積　演習問題

２．運動量保存則

外力が存在しない場合、

運動量の総和は保存されます。

これは、

作用・反作用の力が内部で打ち消し合うため、

全体としての外力が

ゼロになるような状況で利用できます。

運動量保存則は、

力積の関係式から導くことができます。

物体同士が

互いに及ぼし合う力（作用・反作用）が打ち消し合う場合、

運動量保存則が成り立ちます。

この後に学ぶ

エネルギーの演習では、

衝突において

エネルギーが一部失われる（欠損する）ことがありますが、
運動量に欠損はなく、常に保存されます。

X方向の衝突では、
運動量保存則を

そのまま適用して問題ありません。

一方、

Y方向の衝突の場合は注意が必要です。
A・B両物体には、

ともに −Y方向に重力が働いているため、
作用・反作用のように

互いに打ち消し合う外力とはならず、
重力の影響を無視することはできません。

結果から言うと、
衝突の瞬間においては、

重力の影響は無視できます。

理由としては、

・衝突時間が非常に短く
・抗力（衝突による力）と比べて、

　重力は十分に小さいためです。

このため、Y方向であっても、
運動量保存則を適用して問題ありません。

この点について

疑問に思ったことがありますか？
もしそうなら、

それはとても良い観察力の証拠です。

疑問を持てるということは、

現象を深く理解しようとしている証拠でもあります。
とても素晴らしいことです。

はね返り係数の公式について

書き方にはいくつかありますが、

基本的なポイントは以下の通りです。

・B→A、A→B のどちらから見ても

　構いませんが、同じ側から見た

　速度の差をとり、

分数の前には

必ずマイナス（−）を付けてください。

・はね返り係数は、

　「後の速度 / 前の速度」

　で表すことを必ず守りましょう。

この順序を逆にすると、

1より大きくなってしまい、

物理的に不自然な結果になります。
反射すると速度は小さくなることが

感覚的にわかるため、
はね返り係数は 1 未満になると

覚えておくと良いでしょう。

衝突と2体運動について

衝突や2体運動の問題では、

以下の法則を用います。

運動量保存則
はね返り係数の関係式
（後に学ぶ）エネルギー保存則

これらは物理の中でも

出題頻度が高い重要項目です。
確実に理解するために、

しっかりと演習を行いましょう。