ドップラー効果
公式利用
解説
すべてが必須かつ頻出の問題です。
ドップラー効果の公式を
正確に使えるようにしましょう。
また、
自分の問題集や教科書も活用して、
しっかりと確認・復習しておくことが大切です。
a.

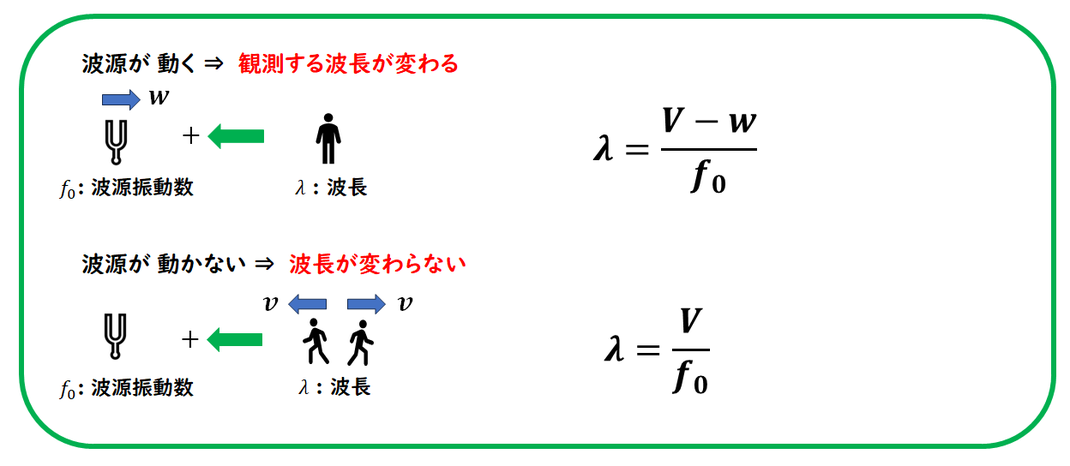
ドップラー効果の公式です。
観測者から見た
波源の方向を正の向き(+)とします。
「観測者 / 振動数」のイメージを持ち、
正しく公式を使えるようにしましょう。
波長が問われることもよくあります。
こちらも公式とあわせて覚えておきましょう。
波長に関しては、
観測者の動きは影響しません。
一方、
波源が動くと波長が変化することを、
しっかりと理解しておきましょう。
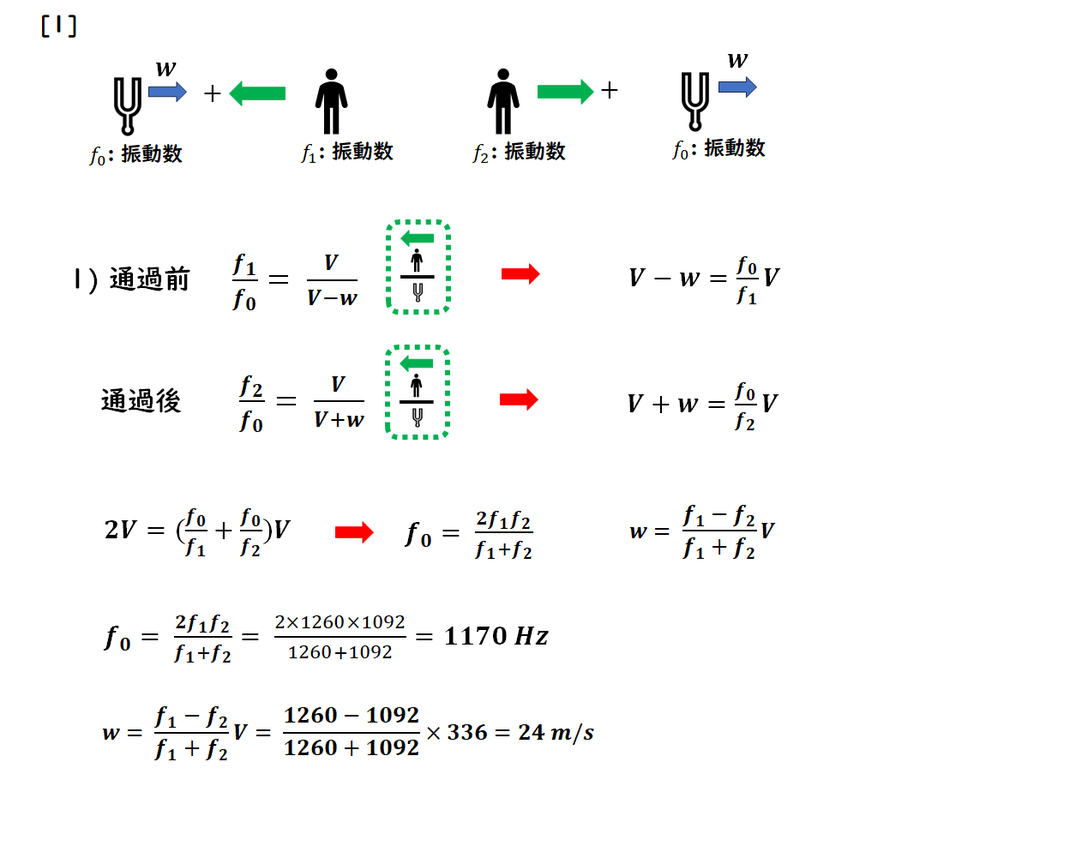
慣れないうちは、
観測者から見た方向に
緑の矢印を描く
ようにしましょう。
この矢印が正しい
正負の判断につながり、
式を正しく立てる助けになります。
式が立てられたら、
f0,w の連立方程式を解きます。
ドップラー効果の問題では、
この式の変形が頻出です。
解の形や変形の流れに
慣れておくことが重要です。
式の意味や変形過程を
感覚的につかめるように
しておきましょう。
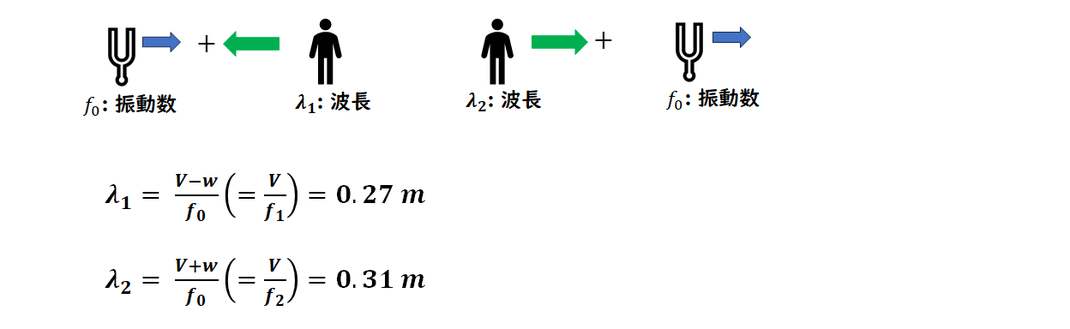
波長を求めます。
今回は
波源が動いているため、
波長は変化します。
ドップラー効果の公式に従って
波長を求めましょう。
また、
先ほど求めた観測される振動数と
波の速度から
波長を計算することも可能です。
ただし注意が必要です。
観測者が動く場合には、
この方法では正しい波長が求められません。
そのため、
原理を正しく理解していない場合は、
この方法は使わないようにしてください。

音源と観測者が同じ向きで、
同じ速さで移動している場合、
観測される振動数は
波源の振動数と等しくなります。
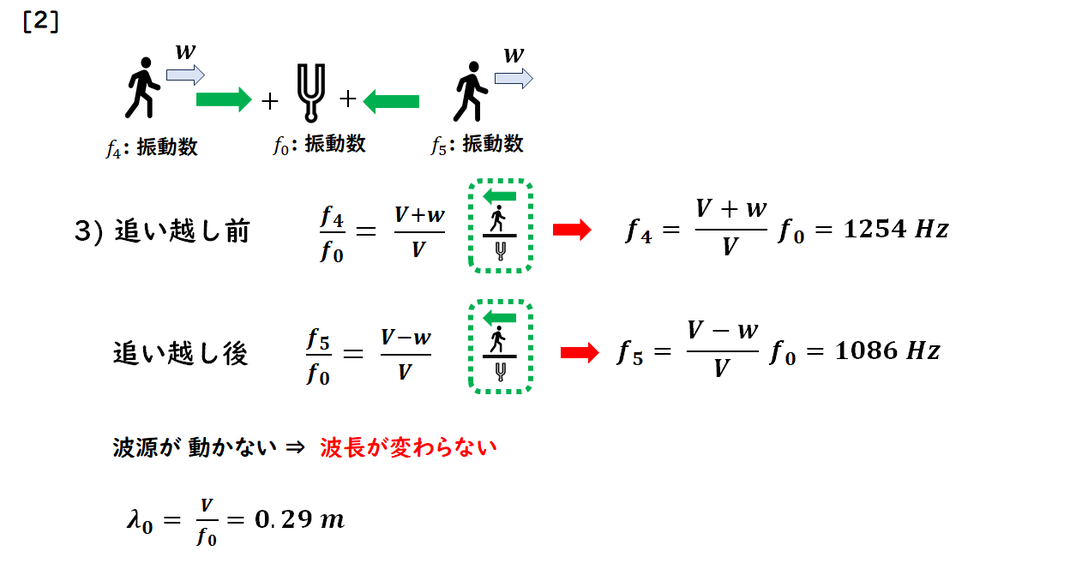
[1] と同様に、
正しく公式を立てて
解答しましょう。
波長は波源が動いていないため、
波源と変わらないことを
正しく覚えておきましょう。
この場合、
観測する振動数から
逆算するのは誤りです。
安易に理解して逆算し、
間違えないように注意しましょう。
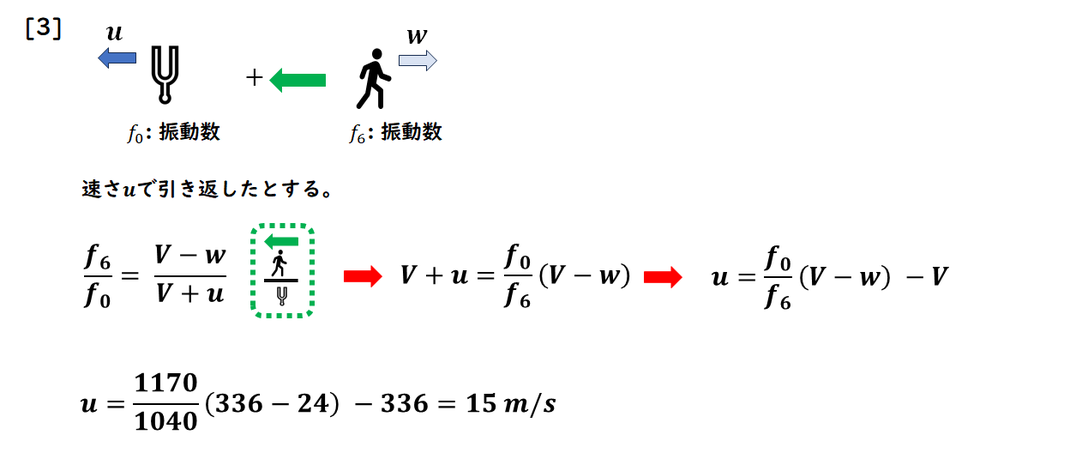
[1][2] 同様に計算します。
音源の速度の向きが
決まらないため、
向きを仮定して求めます。
仮定した向きとは
逆の場合でも問題なく解け、
その際は結果が負の値になります。
b.
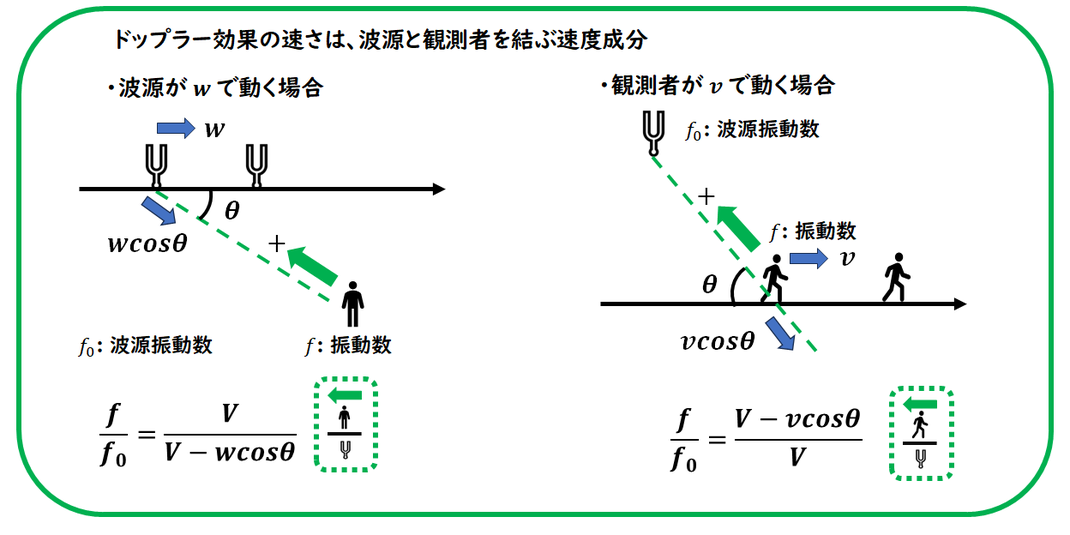
波源または観測者が
異なる方向に動く場合のドップラー効果
波源と観測者を結ぶ直線上の速度成分で考えます。
つまり、運動の速さをその軸に射影した成分を
ドップラー効果における速度として扱います。
運動がこの軸に対して垂直である場合、
ドップラー効果は生じません。
⇒波源の振動数と同じ。
1)
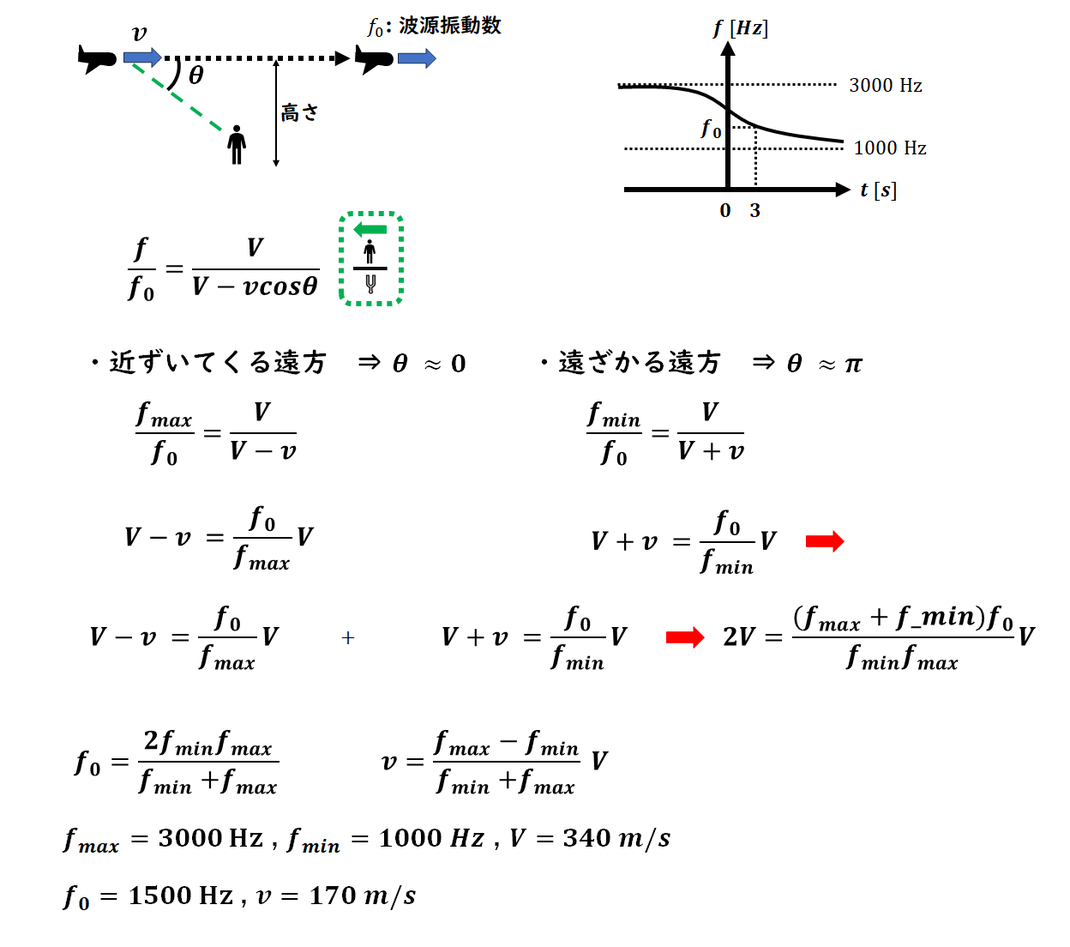
飛行機がある位置にいるときの
観測者が観測する振動数を考えます。
図のように、
飛行機と観測者を結ぶ方向と、
飛行機の進行方向とのなす角を θ とします。
ドップラー効果の公式を用いることで、
観測者が受け取る振動数を
求めることができます。
十分
遠方から接近してくる場合は θ = 0、
飛び去った後は θ = π と
考えられるため、
それぞれの値を式に代入します。
2つの式から、
飛行機の速さと振動数を、
a の問題と
同様の式変形を用いて求めます。
また、観測される振動数は、
グラフから読み取ることができます。
それぞれ代入して答えます。
2)

飛行機と同じ振動数が
観測されるのは、
飛行機が観測者の真上で
音を発したときです。
その音が観測されるのは、
その3秒後です。
音は音速で伝わるため、
このときの
飛行機の高度 は
次のように求められます。
H(高さ) = Vt = 340 × 3 m = 1020 m
3)
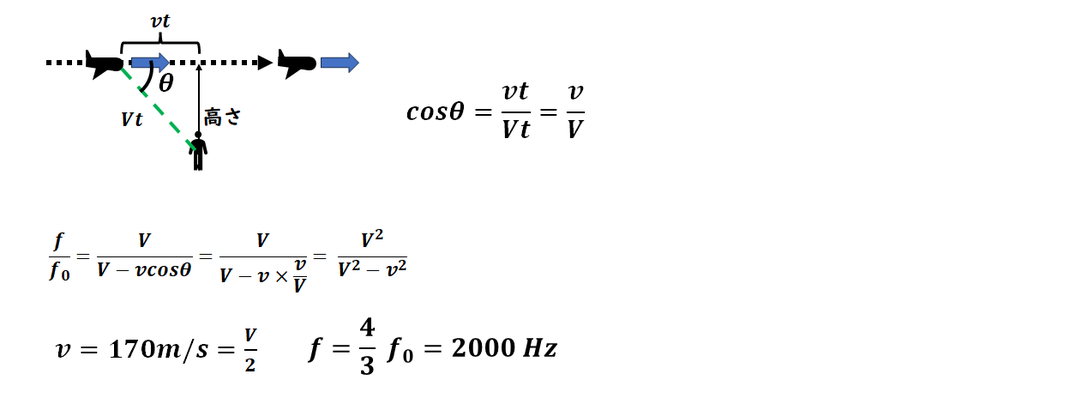
t = 0 に観測される音は、
t 秒前に飛行機が
発した音だと考えましょう。
このとき、
図のような位置関係になります。
・飛行機は、
t 秒前に音を発しているので、
現在の位置から
距離 vt 手前にいたことになります。
・この音が t 秒後に観測されるため、
そのときの飛行機と観測者との距離は
Vt となります。
観測される音の振動数は、
1)の式で(ドップラー効果の式)
で求められますが、
そのためには
cosθ の値が必要です。
cosθ は、図からわかるように
三角比を用いて
計算できるため、
これをもとに
観測される
振動数を求めることができます。
計算の際に、
v = V / 2 と気づけると、
計算が楽になります。
もし今回気づけなかった場合は、
次回は気づけるように、
しっかり復習しておきましょう。
c.
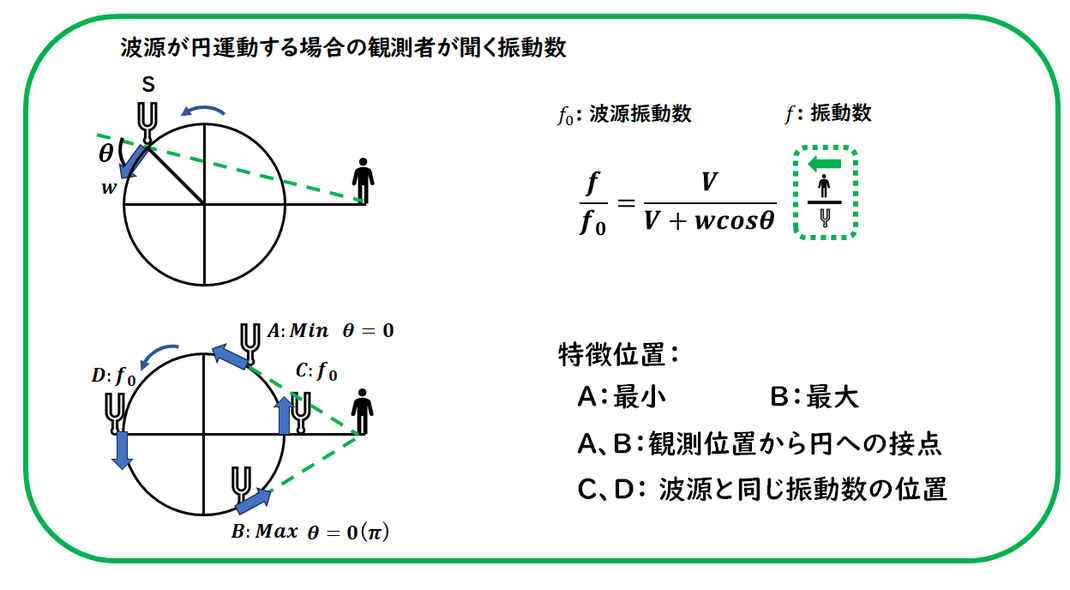
波源が円運動する場合の
ドップラー効果の問題
b. の場合と同様に、
観測される振動数は、
波源と観測者が異なる方向に
動いている場合と同じ考え方で求められます。
特徴的な位置が 4 か所あり、
多くの問題では、
これらの位置で、問われます。
観測される振動数が
最小または最大となる位置は、
観測者から見て、
円運動する軌道に接する位置になります。
この場合、
振動数の式に現れる角度 θ が
0 または π となるため、
数式的にも
その結果と一致します。
最大の振動数となるのは、
速度が観測者に向かう位置で、
最小の振動数となるのは、
速度が観測者から遠ざかる位置です。
感覚的にも納得しやすい関係だと思います。
音源の振動数と、
観測される振動数が等しくなる位置は、
観測者と円の中心を結ぶ直線と、
円軌道との交点上の位置になります。
振動数の式に
現れる角度 θ がπ/2の時です。
1),2)
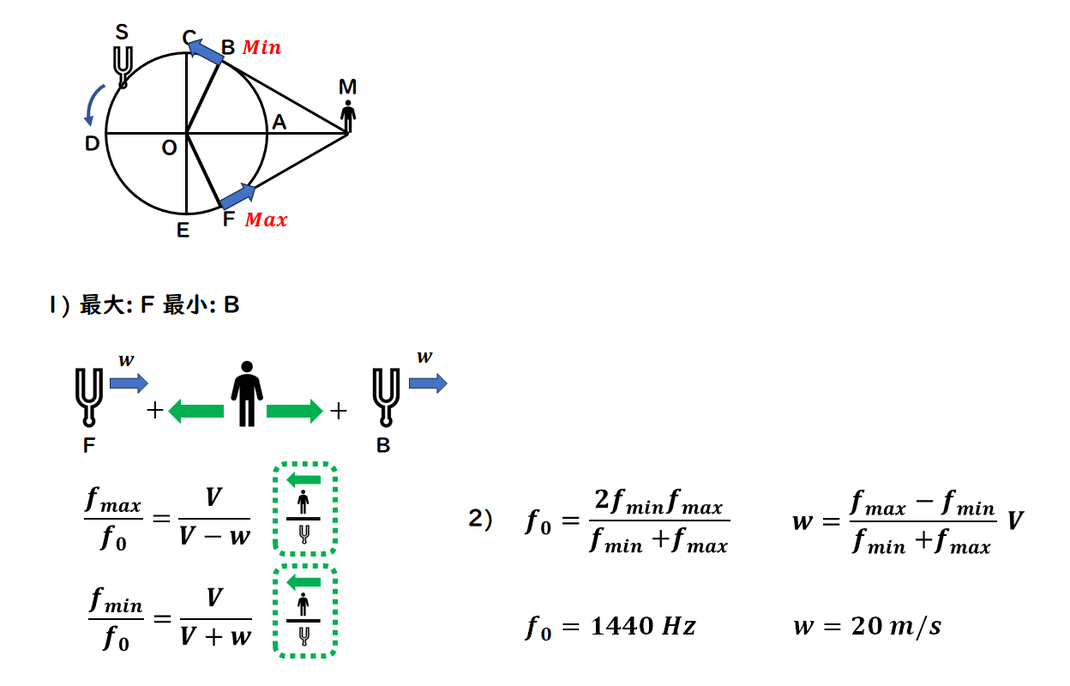
1) は説明の通りです。
2) 速度は観測者と音源を結ぶ方向になるため、
これまでと同様に
ドップラー効果の公式を利用して計算します。
以前の式と同じものが使われるため、
同様に式の変形を行い、解答します。
3)
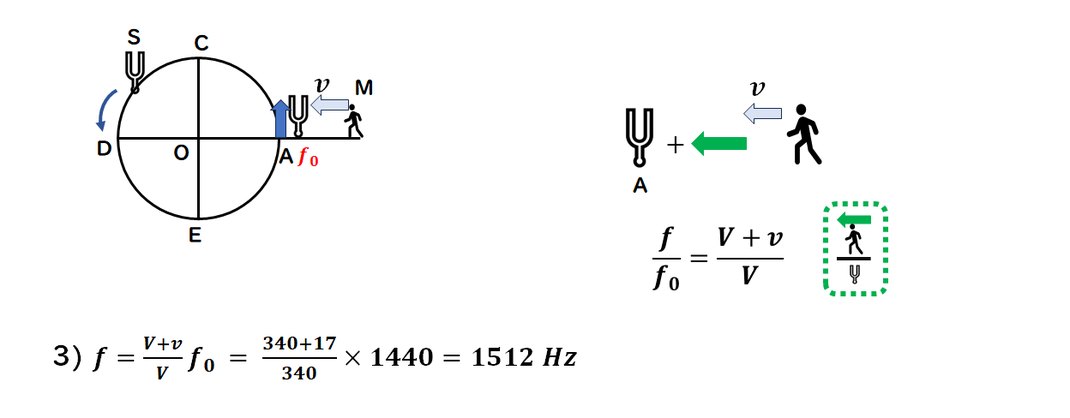
Aで発せられた音の観測振動数は、
波源の振動数と同じです。
この場合、波源は停止しており、
観測者が運動している状況と同じになるため、
波源停止・観測者運動の
ドップラー効果と同じように振動数を求めます。
d.
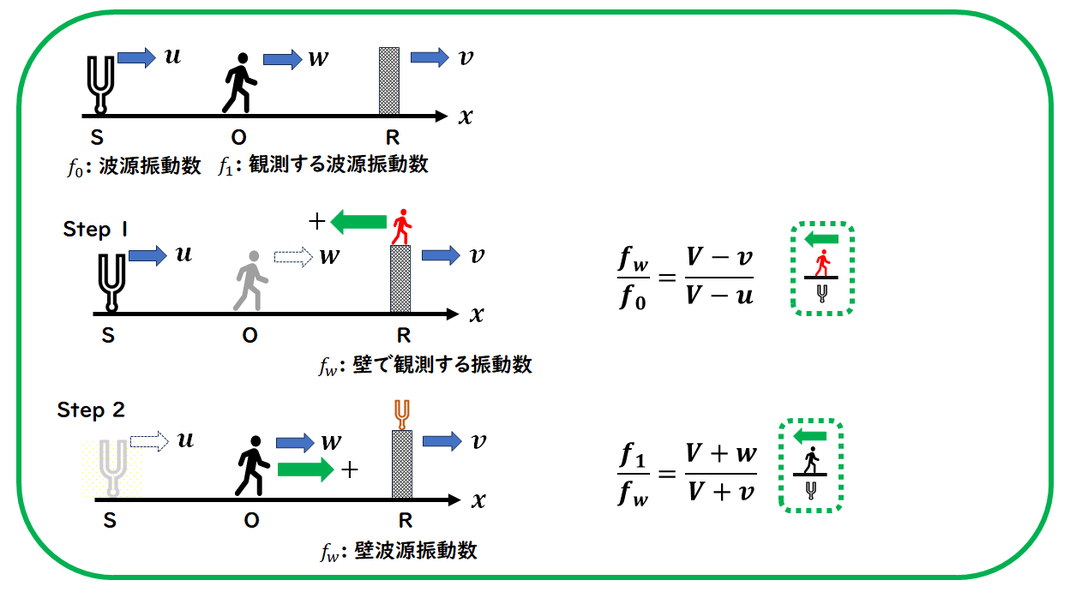
反射に関するドップラー効果の問題です。
この場合、
壁に2つの役割を持たせて考えることで、解くことができます。
Step1 :
壁を観測者とみなし、壁が観測する振動数を求めます。
Step2 :
壁を音源とみなし、観測者が受け取る振動数を求めます。
このような手順で、問題を解いていきます。

うなりの振動数は、
異なる2つの振動数の差の絶対値で求めます。
1)
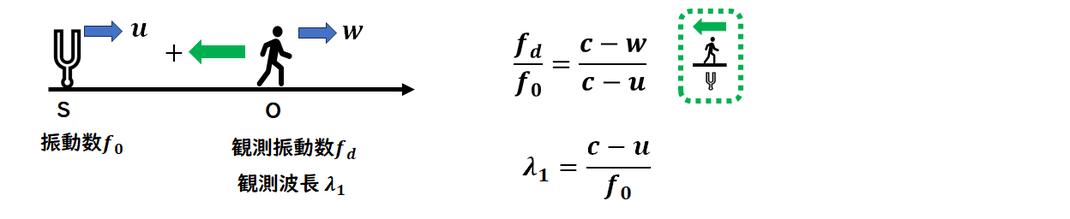
S(音源)と O(観測者)の
ドップラー効果による
振動数と波長を求めます。
波長は、
観測者の動きには影響されないことを
しっかり覚えておきましょう。
2),3)
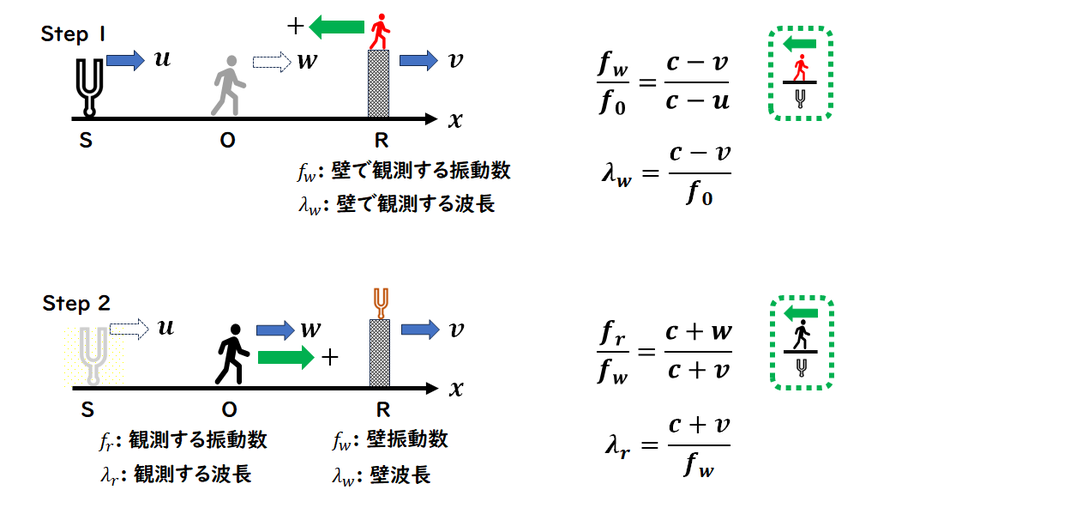
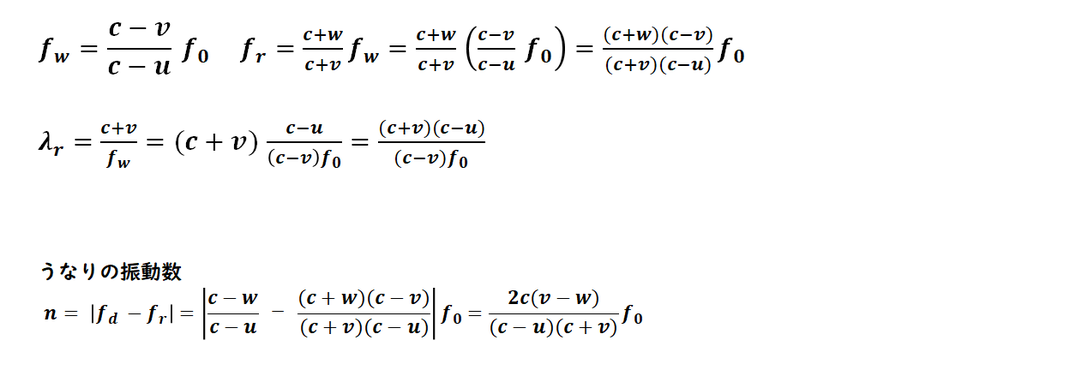
反射に関するドップラー効果の問題です。
Step1、Step2 に分けて、
それぞれ振動数と波長を求めていきます。
うなりの振動数は、
1)の「直接聞こえる音の振動数」と、
2)の「反射して聞こえる音の振動数」との
差の絶対値で求めます。
e.
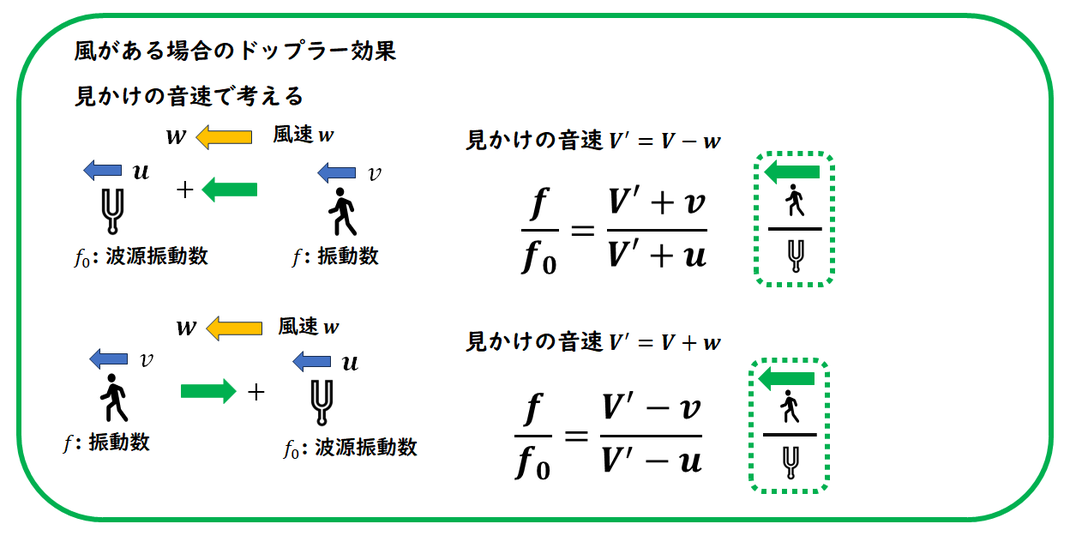
風がある場合のドップラー効果の問題です。
風の影響は、音速に加味されると考えます。
まず、風の速度を加味した見かけの音速を求め、
それを用いてドップラー効果の公式に当てはめることで、
観測される振動数を求めます。
1)
風と反射に関するドップラー効果の問題です。
まず、風の影響を加味した見かけの音速を求め、
その上で、ドップラー効果の公式を利用して振動数を計算します。
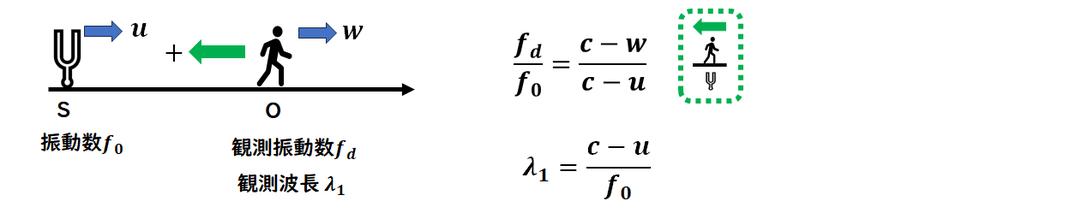
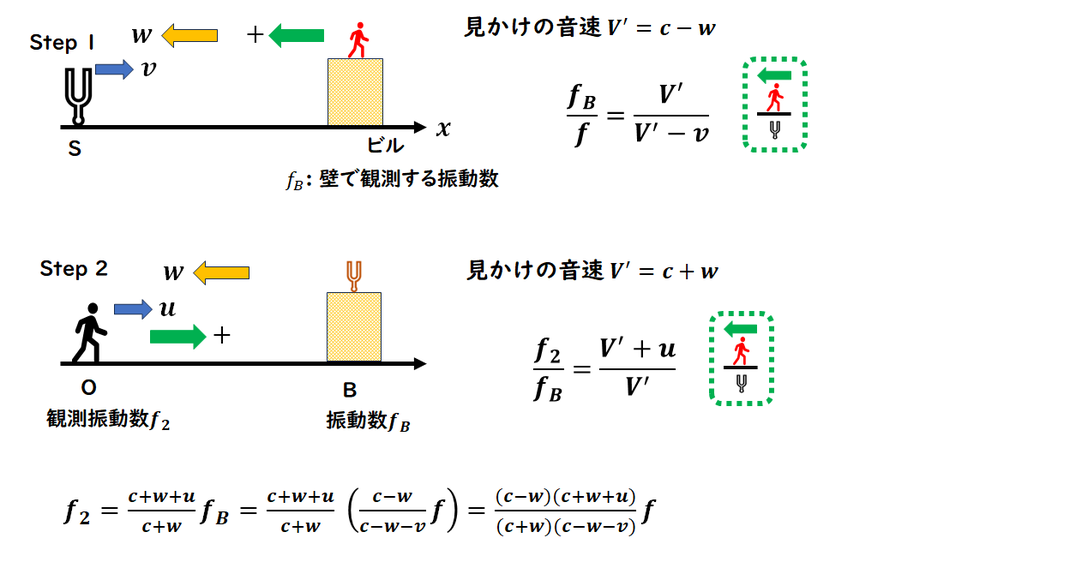
直接聞く振動数と
壁による反射音の振動数を求めます。
2)
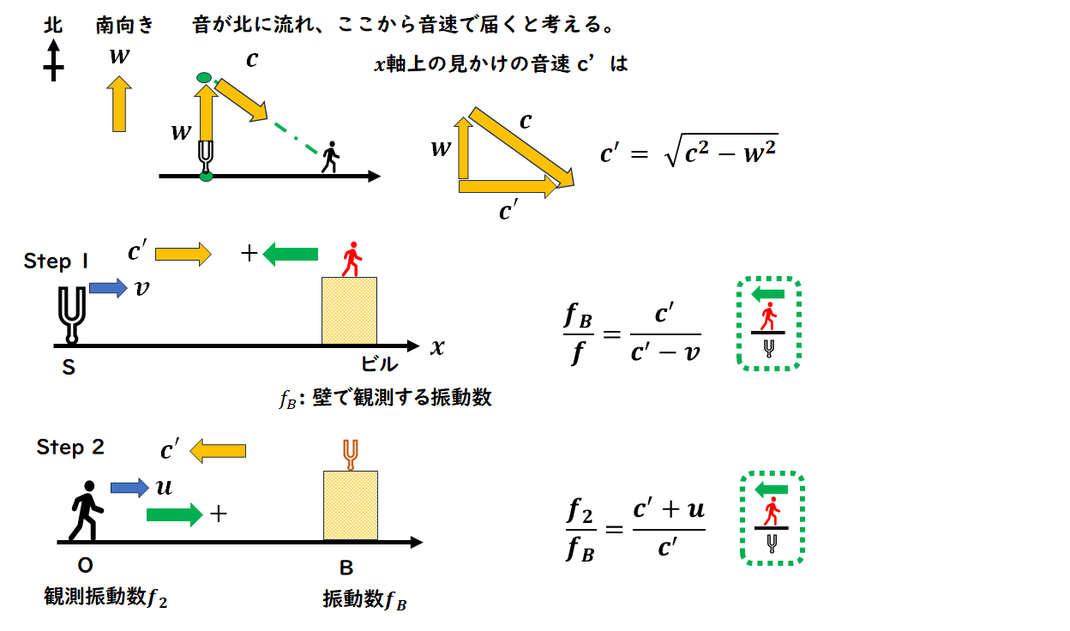
軸と異なる方向に風が吹く場合の
ドップラー効果の問題です。
このような場合は、
風の速度ベクトルを
音源と観測者を結ぶ軸方向に
射影して考えます。
風の速度ベクトルは、
風によって音が運ばれる方向、
すなわち
音源が風に流されて移動したと
仮定したときの位置と、観測者を結ぶ方向になります。
ドップラー効果における見かけの音速は、
この風の速度ベクトルを
音源と観測者を結ぶ軸方向に射影した成分を
見かけの音速として、
ドップラー効果の公式に適用します。
あとは、
見かけの速度が変わるだけで、1)と同じです。
ドップラー効果を利用した典型的な問題でした。
ドップラー効果の公式を正しく覚えていれば、
十分に解くことができると思います。
公式を正しく理解し、正確に使いこなせるようになるまで、
しっかりと演習を重ねることが大切です。
