ドップラー効果
原理 解説
ドップラー効果の公式を導く問題です。
このような問題では、
自分の知っている方法で導くのではなく、
問題の誘導に従って解答する必要があることに注意してください。
この問題は、
ドップラー効果の公式を覚えるための
補助問題ではないという点を理解しておきましょう。
なお、
ドップラー効果の公式そのものは、
原則として覚えるべき内容です。
ドップラー効果の公式を導く問題には、
主に3つのパターンがあります。
試験本番でそれぞれに対応するのは、
簡単ではありません。
どのパターンにも確実に対応できるよう、
あらかじめ十分に演習しておくことが重要です。
a.
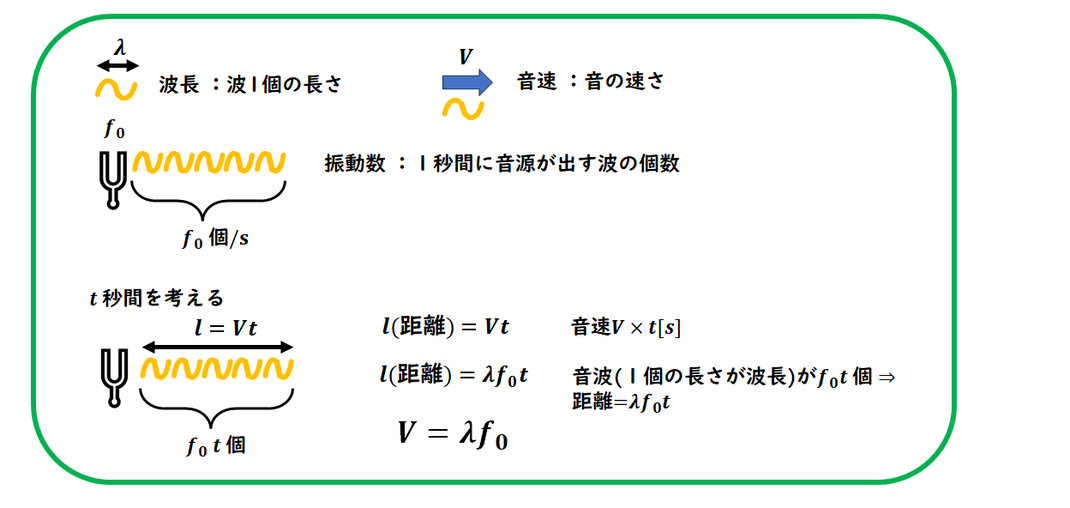
波長や振動数を「波の個数」
として捉える問題です。
最もよく出題されるタイプであり、
波の数を数えることがポイントになります。
たとえ公式「λ = V / f」を知っていても、
それだけでは解けません。
公式の意味をしっかり理解し、
実感を持って捉えることが大切です。
動かないときの
各パラメータの意味
波長(λ):波1つ分の長さ
振動数(f):1秒間に届く波の個数
音速(V):音が進む速さ(1秒間に進む距離)
音源が t秒間 音を出したとします。
音が伝わった距離は
l = Vt
この間に出た波の個数は
N = ft
1つの波の長さが λ なので、
波全体の長さは
λ × N = λft
波の長さ全体と
伝わった距離は等しいため
l = λft=Vt
このようにして、
V = λf が導かれます。
この方法を使って、
音源が動く場合や観測者が動く場合に、
観測者が聞く音の振動数(ドップラー効果)を求めます。
[1] 動かない場合
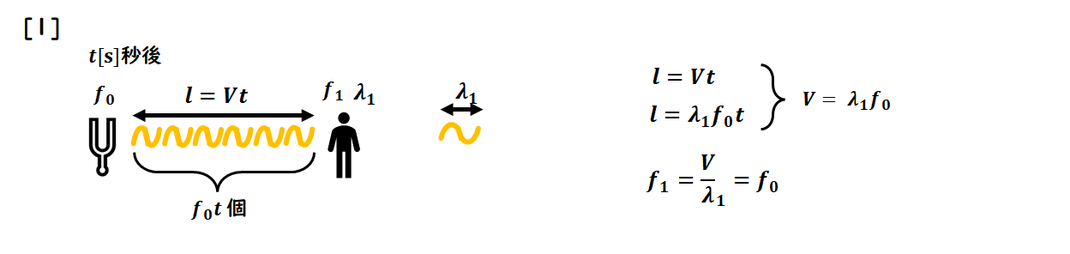
説明の内容に従い、
問題文の指示どおり
計算を進めてください。
[2]音源が動く場合
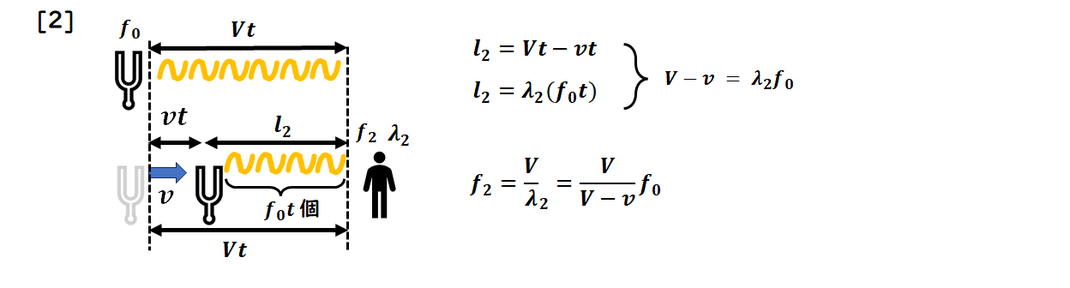
音源が動いている場合、
音源はf0 t 個の波を発しており、
また音源が動くことで
観測者との距離が短くなる点に
注意して計算します。
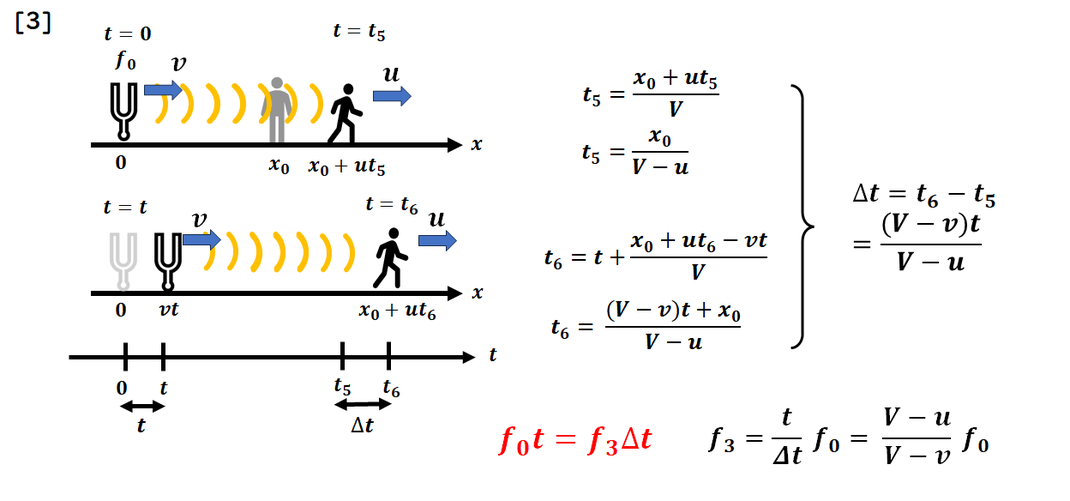
[3] 観測者が動く場合
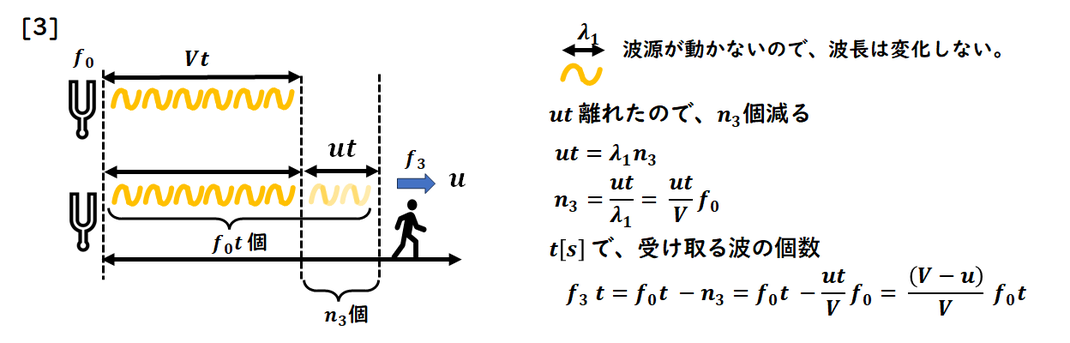
この問題において、
観測者が動く場合は
扱いにくいポイントとなります。
この場合、
波長は変化しないことを覚えましょう。
そのため、観測者が動くことで
受け取る波の数に増減が生じます。
この増減を元の振動数 f0に加味して、
振動数を求めます。
振動数の増減は、
観測者の移動距離を
波長で割ることで計算できます。
この例では
観測者が遠ざかる場合なので、
差として扱いますが、
近づく場合は和として計算します。
[4] 音源が動き、観測者も動く
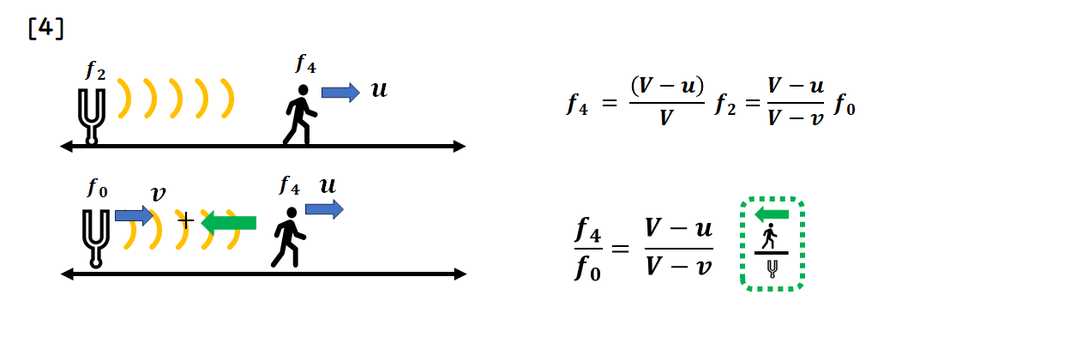
図[2]や[3]のように
視覚的に求める方法もありますが、
ここでは問題文に従い、
音源が止まっていると仮定します。
そのため、元の振動数f0 ではなく、
振動数 f2を発していると考え、
[3]のような、
観測者が動く場合の振動数を求めます。
最後に、公式とあっているか
確認します。
b.
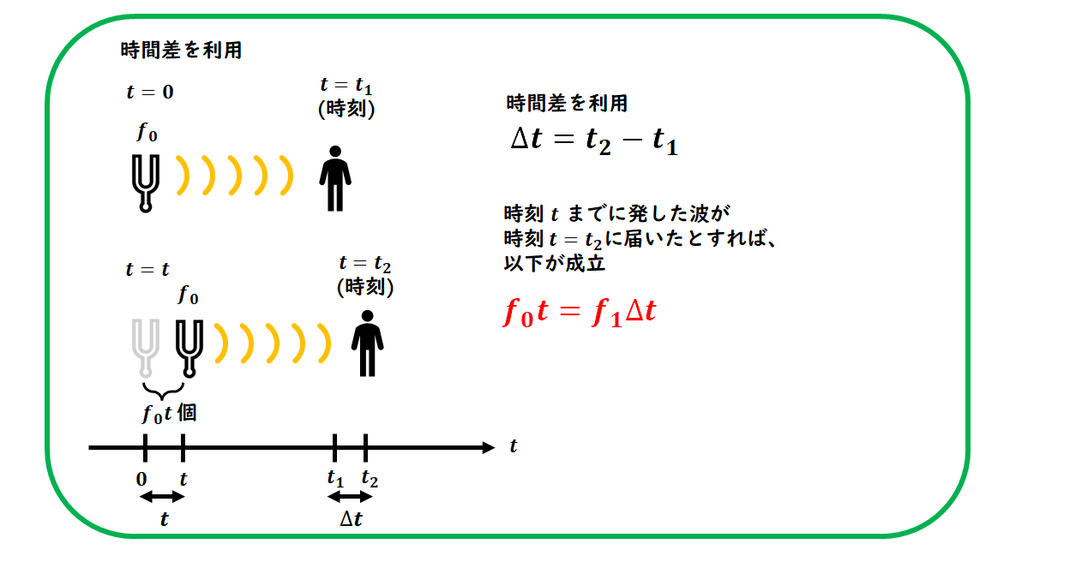
ドップラー効果が起こった時刻を求め、
ドップラー効果が起こっていない場合の
時刻との差から、
ドップラー効果を求める問題です。
この方法は、
今回のような直線上の場合に限らず、
斜め方向や風の影響がある場合でも、
ドップラー効果の式を導く際に
よく出題されます。
ポイントはいくつかありますが、
特に「時刻」と「時間」の
区別をすることが、
混乱を招く重要なポイントです。
整理して解くようにしましょう。
後半の時刻t に発した波が
時刻 t2 に届くため、
t2=t+(t2−t) の時間となります。
このように「t+」の和を計算することを
忘れないようにしましょう。
最後に、
時刻t までに発せられた波の個数が、
tt 〜 t2 の間に観測者が受け取る波の数
fΔt となります。
この 赤字部分 をしっかり理解し、
確実に使えるようにしましょう。
この問題では、
赤字部分 を感覚的に
思い出せるよう演習しましょう。
このタイプの問題では、
Δtを1sや周期Tで扱うことが
よくありますが、仕組みは同じです。
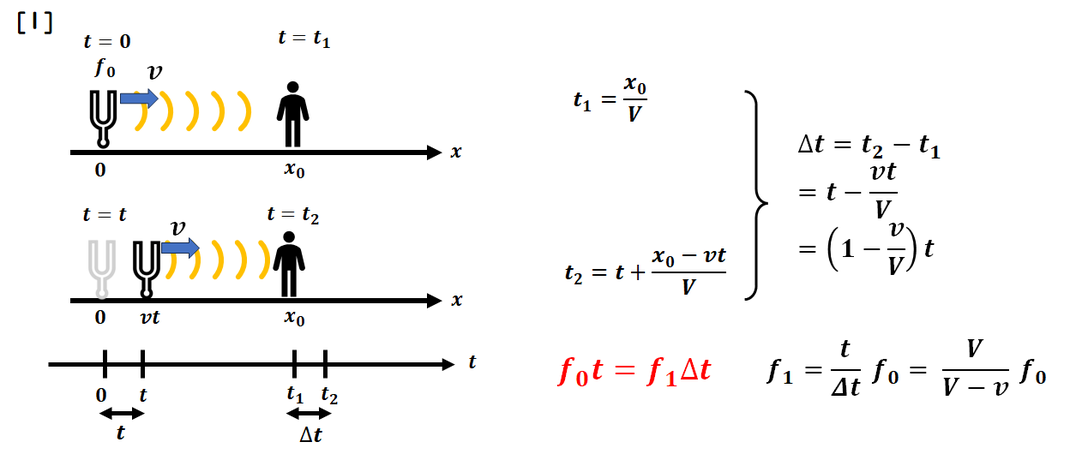
t2 の時刻の計算と
振動数の関係の
赤字部分を利用して
問題を解きます。
一つ一つ丁寧に考えていけば、
理解できると思います。
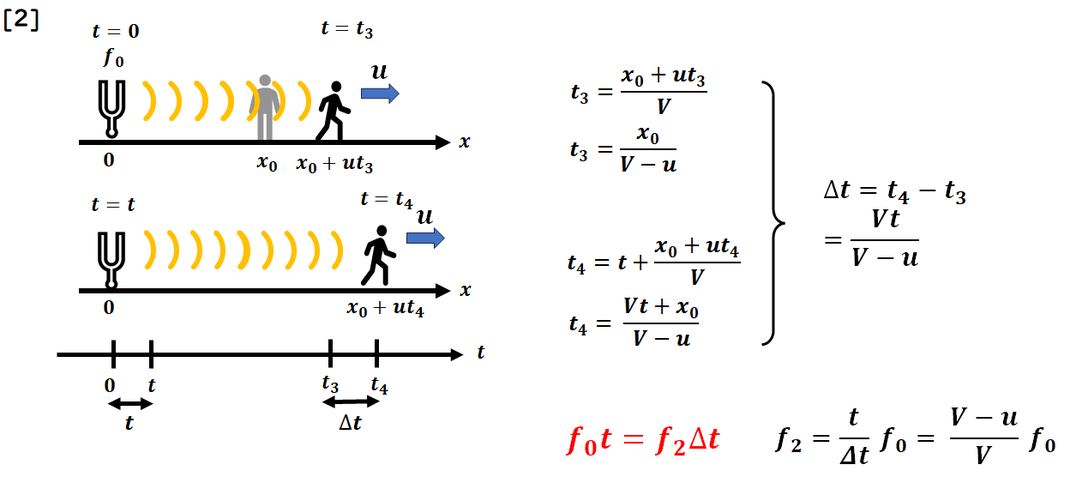
同じように解きましょう。
時刻t3,t4であることに
であることに
気をつけましょう。
[1] [2] と同じようにして
計算しましょう。
c.
この問題は、
波の式をもとに
ドップラー効果の式を導くものです。
波の式の基本的な理解と、
前問 a・b をしっかり押さえていれば、
十分に解ける内容です。
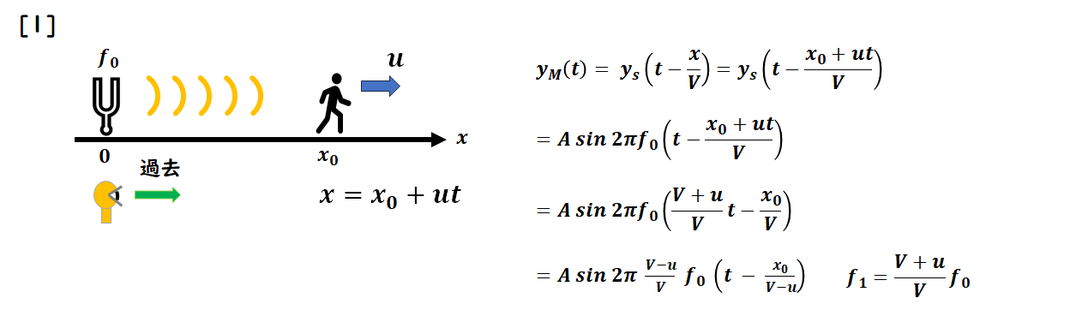
O が観測する波y(x,t) を、
x=0の波y(0,t)を利用して
求める問題です。
ドップラー効果の考え方では、
時刻t において観測者O は
速度vで移動しているため、
位置はx=x0+vt とする
必要があります。
位置 x=0 から
位置x を見ると、
それは過去の位置に相当するため、
波がx に届くまでの時間、
つまり x / V を
引けばよいことになります。
観測される振動数は、
波の時間変化の項 2πft をもとに、
実際に観測されるfと
比較することで導きます。
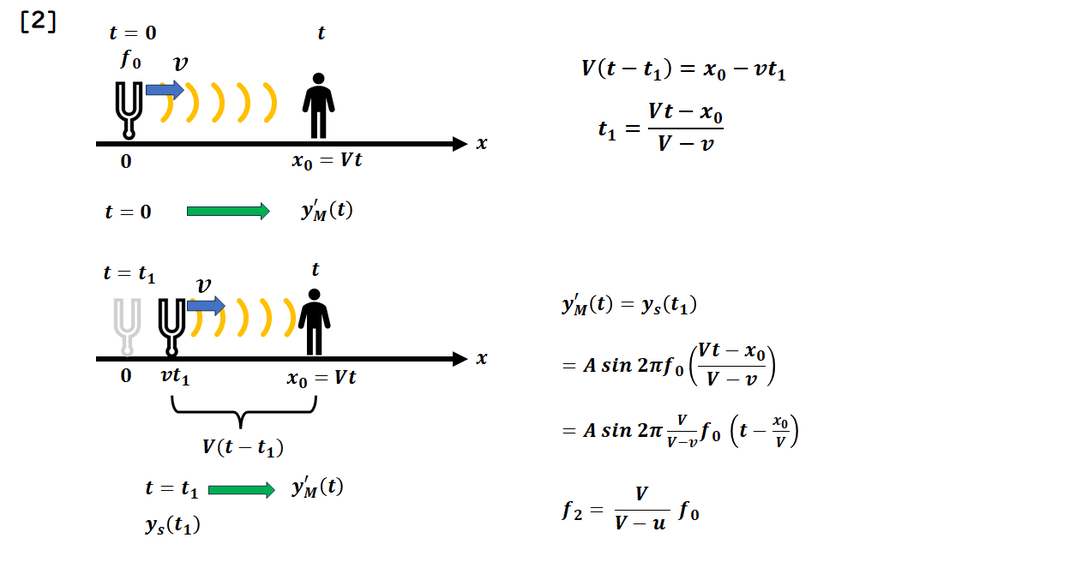
問題文にある
”t=t1 で発した波が、
観測者の受け取る波の変位になる”
という関係、すなわち
ys(t1) = y'M(t)
が読み取れれば十分です。
時刻 t1 に関する関係式は、
b.の問題の
復習にもなっています。
あとは、それぞれの設問について、
問題文に従って求めていきましょう。
ドップラー効果の公式を
求める問題でした。
b,c の問題は、
初見では難しいことが多く、
何度か繰り返し練習しておく必要があります。
また、たとえ解いたことがあっても、
「公式を導く問題である」という
意識を持って取り組むことが大切です。
わかりにくい問題でもあるので、
お手持ちの問題集に類題があれば、
併せて「どのパターンに当てはまるか」を
意識して、解けるようにしておきましょう。
