波動基本問題
解説
a・b・c・d:基本問題
e・f:標準問題
波動のグラフ・式・パラメータにしっかり慣れておきましょう。
特に、反射に関する式の立て方については、
三角関数の操作と合わせて確実にできるようにしておくことが大切です。
a.
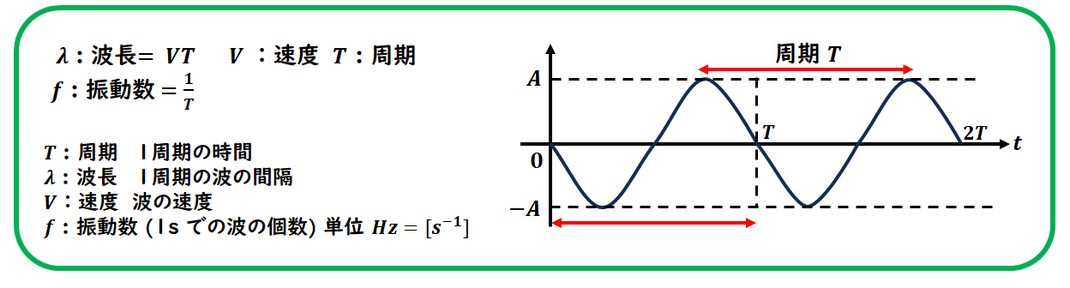
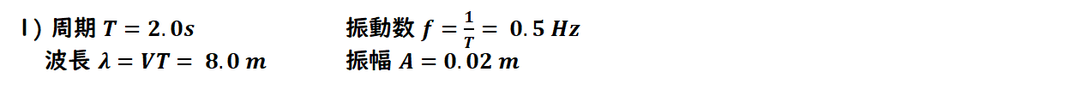
横軸が時間であることを確認すると
周期が求まります。
波動のパラメータから
求められます。
2)
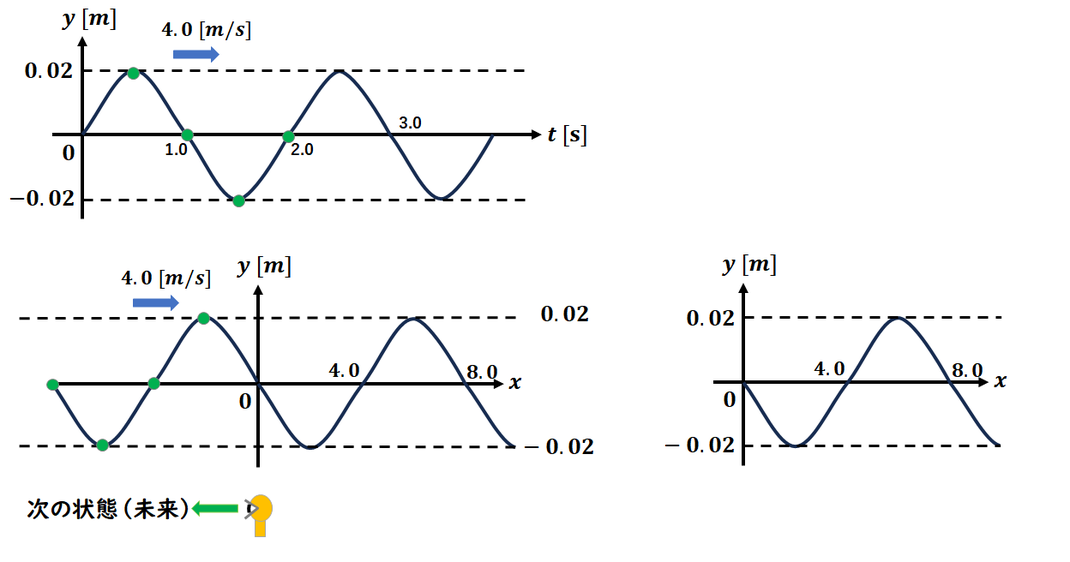
t = 0 での y-x グラフを作図する問題です。
時間のグラフから以下の情報が読み取れます:
-
t = 0.5(= T/4)で山(最大振幅)
-
t = 1.0(= T/2)で y = 0
-
t = 1.5(= 3T/4)で谷(最小振幅)
-
t = 2.0(= T)で再び y = 0
この情報をもとに、x = 0 から
未来側(波が進む方向)の位置における
変位を考えてグラフを作成します。
そのまま正の x 軸方向に延長することで、
t = 0 の時刻における y-x グラフを描くことができます。
3),4)
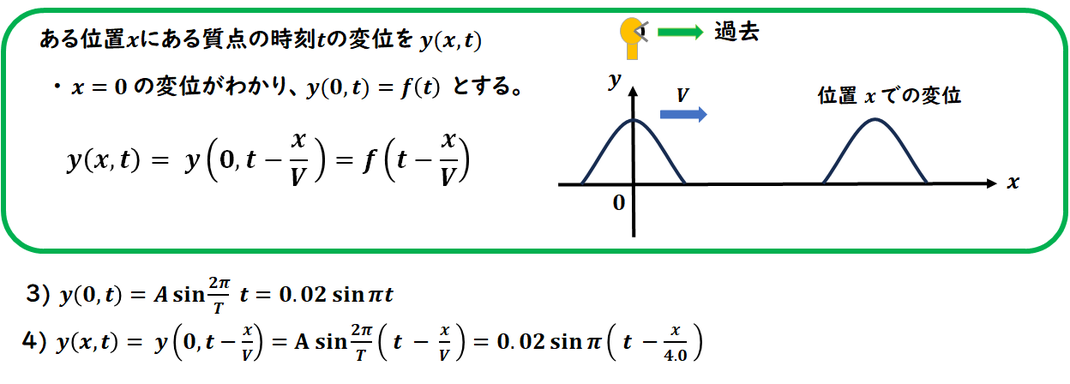
波動を式化する問題です。
3)は問題の図を式化すればよいです。
4)xでの式化です。
x=0からxまでの時間を考えて
過去位置or未来位置になるかを
考えます。
この問題はxは過去位置なので、
引けばよいことになります。
5)

単振動の位置を求める問題です。
速度最大位置なので、
y=0で、のちに山になる
位置を求めればよいことになります。
6)
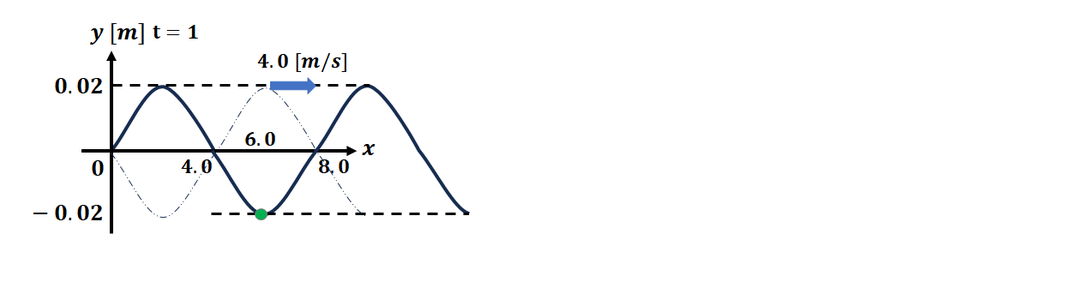
t = 1 で、
加速度が最大となる位置を求める問題です。
まず、t = 1 での位置のグラフを考えます。
波は速度 4 m/s で進行しているため、
x = 4 × 1 = 4 m
分だけ波が進んでいます。
つまり、
t = 0 の y-x グラフを
右に 4 m 平行移動すれば、
t = 1 のグラフになります。
次に、加速度の大きさに注目します。
加速度は
ma = -kx
に従うので、
加速度の大きさが最大になるのは、
変位(x)が最大または最小のときです。
よって、位置が最小のとき(=谷の位置)、
加速度は最大になります。
この谷の位置をグラフから読み取り、
それが解答になります。
b.
1)~3)
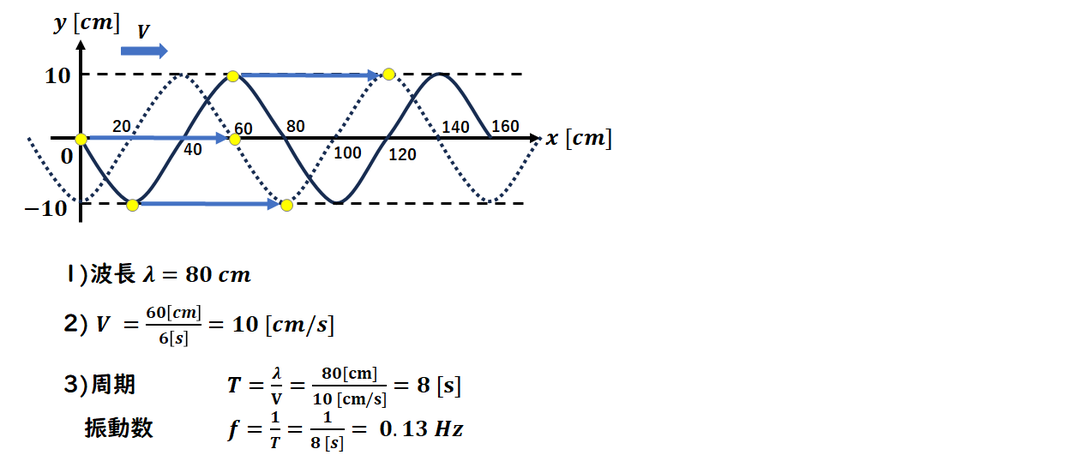
グラフから読み取る問題です。
1) 横軸がxなので、波長が読み取れます。
2) 速さを求める問題です。
波が点線まで移動するのにかかった
時間は 6 秒です。
したがって、
速さを求めるには、
この間に移動した距離を
調べればよいことになります。
参照点は、
実線上のどの点を選んでも構いません。
その点を、
波の進行方向に沿って点線上まで動かしたとき、
ぶつかる対応点との距離が移動距離になります。
この方法で調べると、
移動距離は 60 cm だとわかります。
あとは速さを計算します。
速さ=移動距離/時間=10 cm/s
3) パラメータの計算で、
周期Tが求まり、振動数fが求まります。
4)
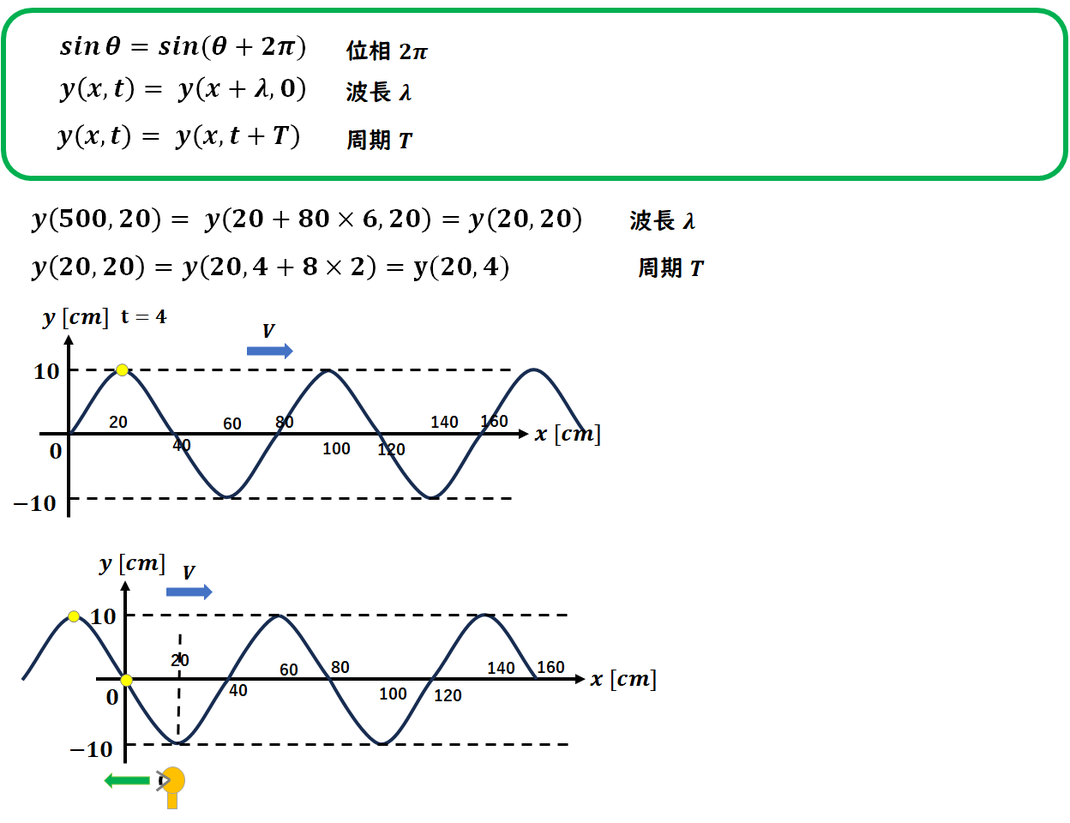
t = 20 s での x = 500 の
y の変位を求める問題です。
波動の性質として、
-
位置方向には波長ごとに、
-
時間方向には周期ごとに、
波の形が繰り返されることを利用します。
この性質を使って、
図の範囲内で同じ波の状態になる
時刻と位置に変換して求めることができます。
x= 20,t=4の時の変位を求めれば
よいことになります。
方法を2通りで求めます。
ⅰ) t=4のグラフを図示して
求めます。t=4だと
x=10×4 = 40cm 移動させます。
この図からx=20の変位を
読み取ります。
ⅱ) t=0のグラフから求めます。
t=4はT/2より半波長分遅れた
位置が答える位置になります。
x=20からλ/2先の位置を
読み取ります。
5)
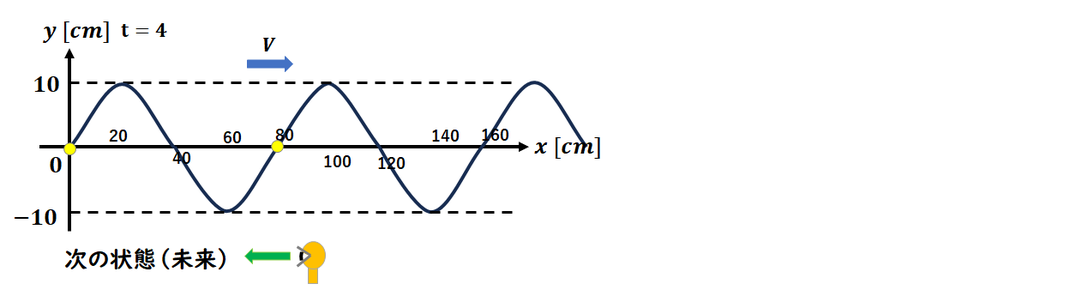
t=20s後は、
4)からt=4s後と同じなので
t=4sのグラフを描き、
速度最小位置を求めます。
c.
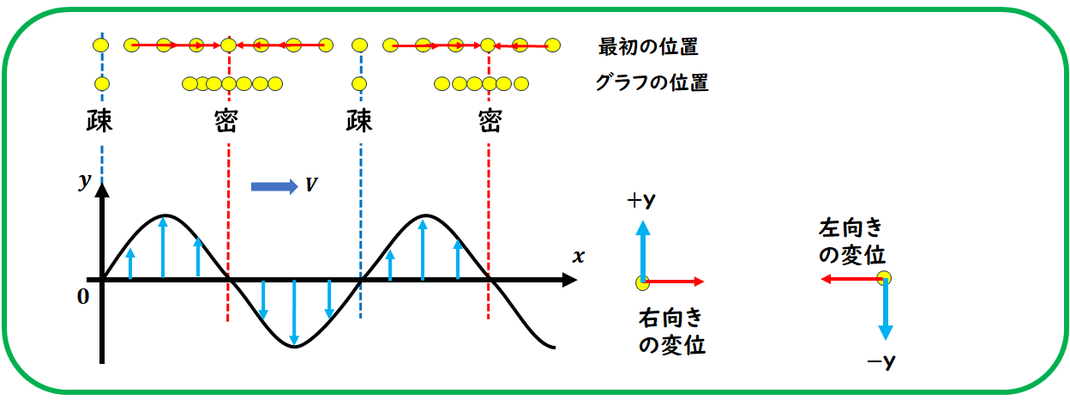
縦波の問題です。
縦波の問題は、横波に変換して
考えるのが基本です。
特に、疎(まばら)・密(密集)の位置を
問う問題が多く出題されます。
それ以外の部分は、
横波の問題と同様に解いて問題ありません。
まずは、縦波=疎密の波で
あることを意識しながら、
横波としての視点から
波の動きを捉えていきましょう。
1) ~ 3)
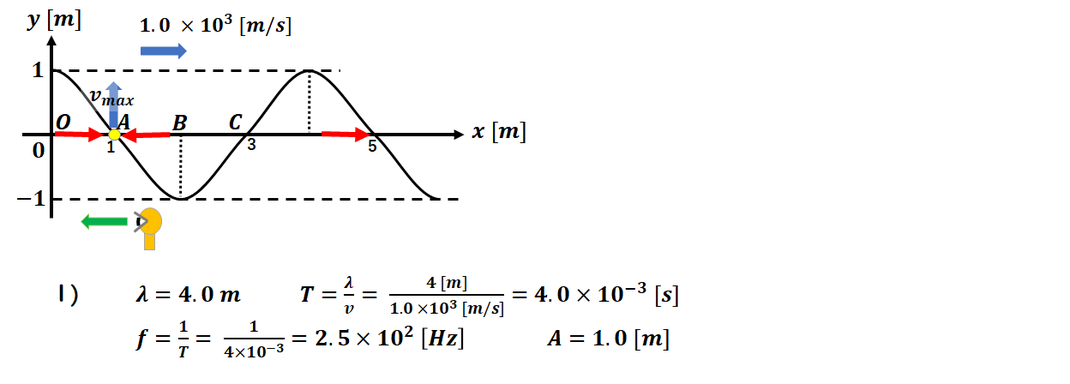
1) グラフから読み取る問題です。
横軸xなので、
波長が求まります。
そのままは求まらず、
λ/4 = 1.0m が読み取れます。
λ = 4.0 m になります。
後は他と同様です。
2) 密を求める問題です。
図の赤矢印を描いて、
集まる場所が密です。
なので、Aになります。
3) 速度最大は
ほかの問題と同じです。
未来方向が分かれば、
Aとわかります。
4)
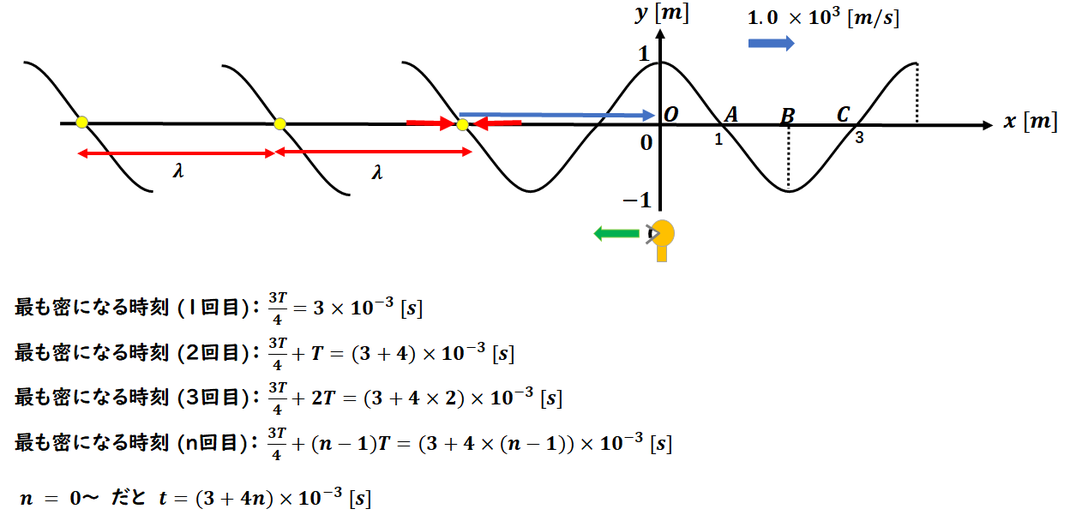
「密」になる時間の求め方
「密」になる時間とは、
密の位置が O(観測点)に
到達する時間のことです。
波が 左から右に進んでいるなら、
未来の波は左側にあると考えます。
未来は左なので、
まず、密の位置を探します。
密の位置は3λ/4=-3mの位置なので、
Oにたどり着く時間を
計算します。
波は周期的に Oに到達するため、
最初に到達する時刻に周期 Tを加えた時刻
にも、再び同じ状態になります。
したがって、
最初の到達時刻だけでなく、
周期を加えた時刻も考慮する必要があります。
この点を忘れないようにして、
正しく時間を求めましょう。
n は整数なので、n = 0 からとしています。
ただし、n = 1 からとして (4n−1)と解答した場合も、
本質的には正しいため、問題ありません。
ただし、本番の試験では
問題文の条件(整数か自然数か)に注意して、
どこから
数え始めるかを正しく判断しましょう。
自然数として
指定されていれば、n = 1 からで正解です。
過去の方向から1回目を計算して
周期的に求めても良いと思います。
d.
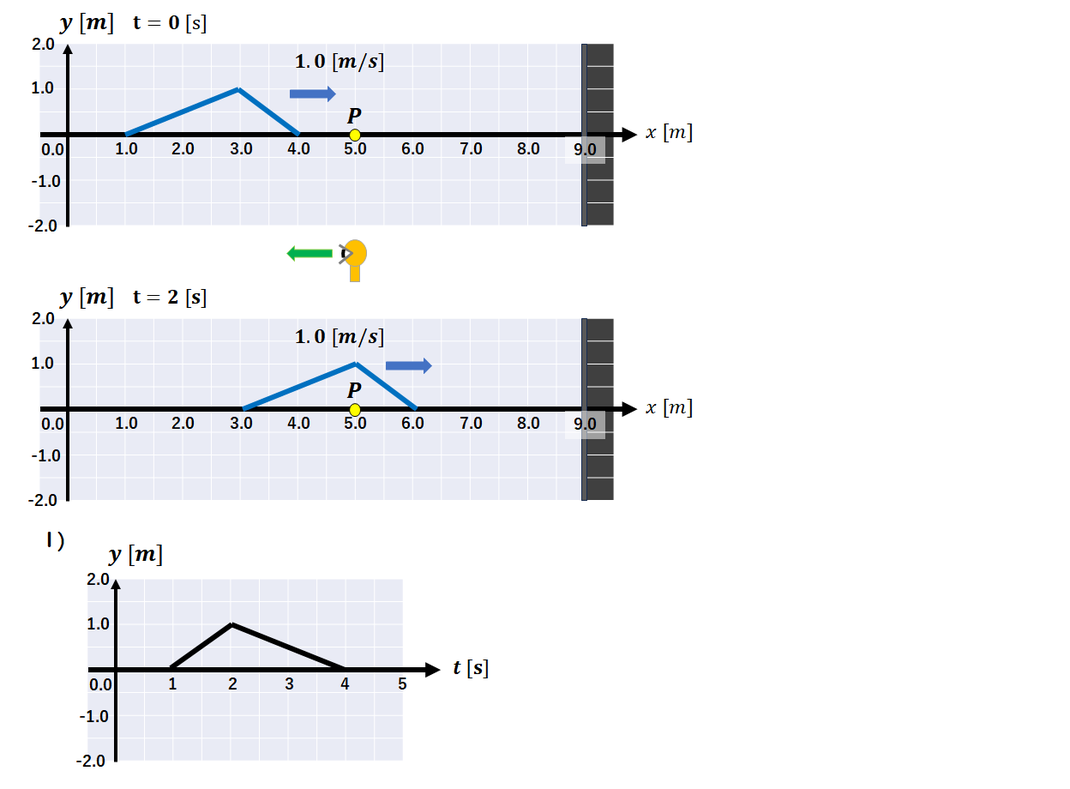
P(x=5)におけるy-tグラフ
を描く問題です。
波は左から伝わってきます。
各時刻(1秒ごと)における
点 P のy の変位を求め、
それをもとに
y-t グラフを作成します。
図は t = 2 秒 のときの
波の様子を示しており
このとき点 P における
y の変位は 1 です
2),3)

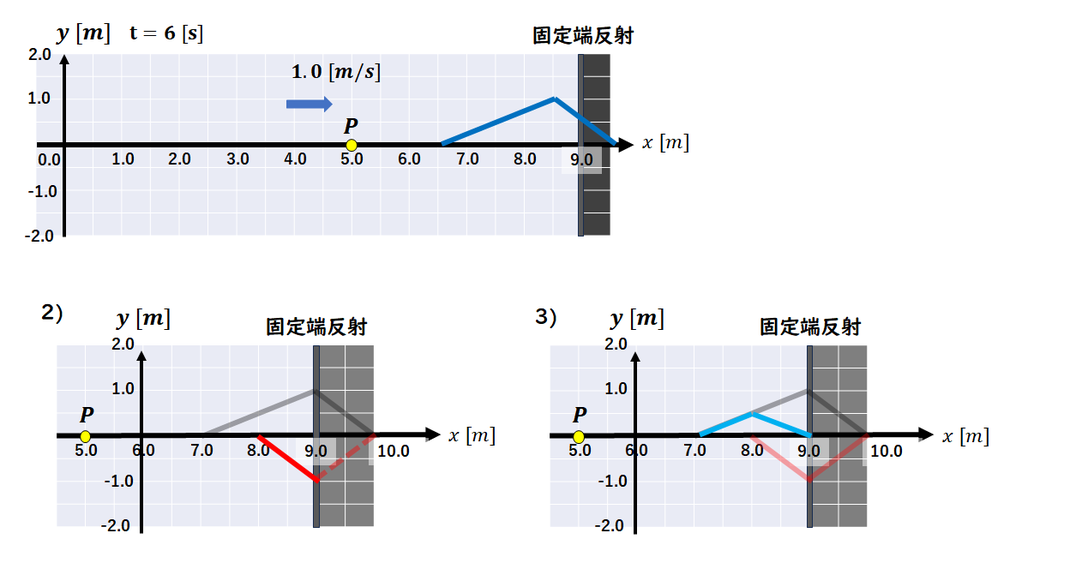
固定端反射による
合成波の作図問題です。
時刻は t = 6 秒 なので、
この時刻における
波の様子を描きます。
反射波は、入射波を反転させて
折り返すことで作図します。
(固定端では、合成波が
節になることがポイントです)
最後に、
入射波と反射波を
重ね合わせて合成波を描きます。
e.
自由端反射による
合成波を式で表す問題です。
手順をしっかりと覚え、
正確に式を
立てられるようにしましょう。
計算はやや複雑ですが、
丁寧に処理すれば確実に解けます。
この分野は苦手とする人も多く、
差がつきやすいところです。
しっかり演習して、
得点源にできるようにしましょう。
[1]

(1)
図は y-t グラフを表しています。
グラフから周期は 4T と読み取れます。
また、問題文から波の速さ v を
求めることができます。
速さと周期がわかれば、
波長λも求まります。
(2)
図の y-t グラフから、
変位 y を時間 t の関数として
式に表しましょう。
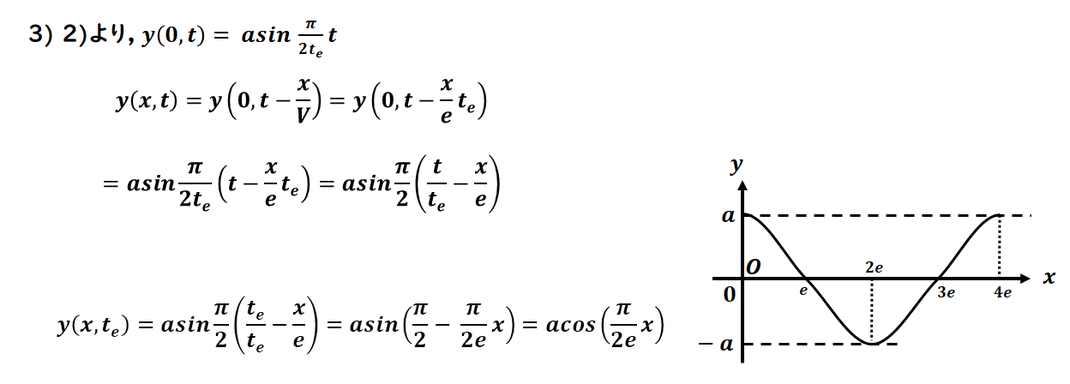
2) より、x = 0 における時間変化
y(0, t) が求まりました。
この結果をもとに、
波が +x 方向に進む場合の、
任意の位置 x における
波の変位 y(x, t) を表す式を
導くことができます。
後半の t=te における
波動 y1 は、
関数 y(x,te) を計算して求め、
グラフに表します。
[2]

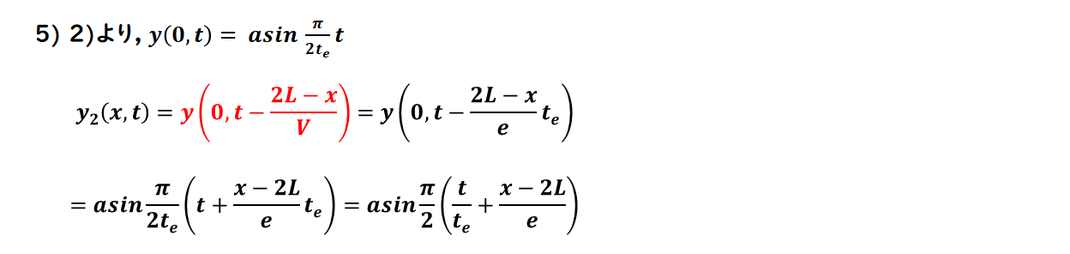
5)
反射波を式で表します。
反射波は、x=L で自由端反射した波です。
自由端反射では変位の符号が
反転しないことを踏まえて、
説明図に従って、
反射波の式を導出します。
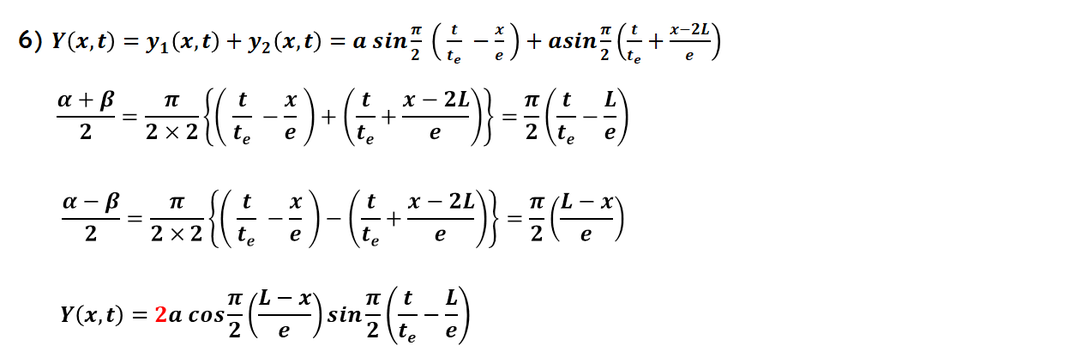
6)
合成波を求めます。
入射波と反射波を合成して、
合成波の式を求めます。
計算は丁寧に行い、
符号や三角関数の扱いで
間違えないように注意しましょう。

6) の結果から、
振幅 > 0 を示します。
合成波の式をもとに、
合成された波の振幅が正である
(0より大きい)ことを確認します。
これは、
入射波と反射波が完全に
打ち消し合っていないことを意味します。
f.
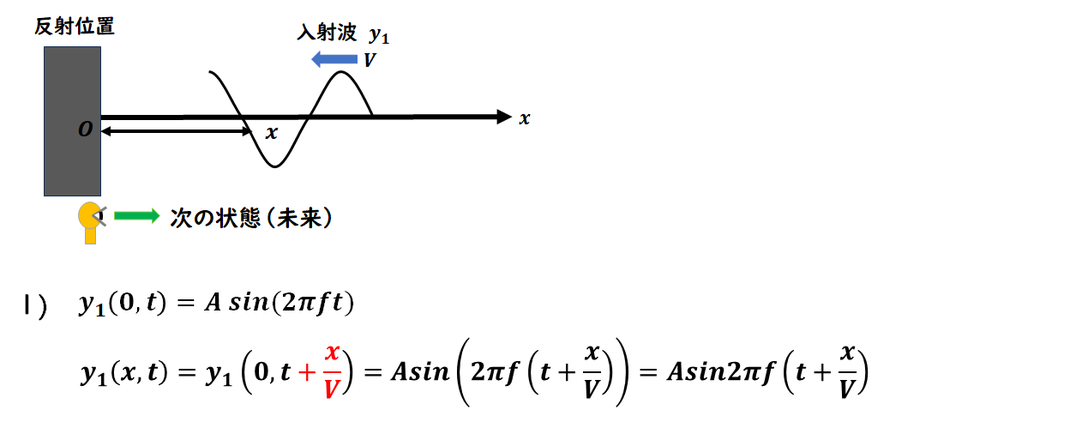
公式に頼りすぎると間違える問題です。
今回は 負の方向(-x方向)に進む波 を考えます。
波は 未来に向かって進む現象 です。
したがって、
波が 負の方向(左)へ進む
⇒ 時間が進むと、波形は左へ移動
よって、
未来は
「t+x/V」
で記述される
このことに気をつけて、
式を立てましょう。
波の向きと未来の方向を気にしながら
式に落とし込めると、
ミスがぐっと減りますよ。

固定端反射の場合、
反射点での合成波の変位は
0 になります。
この条件をもとに、
x=0での反射波の時間変位
を求めます。
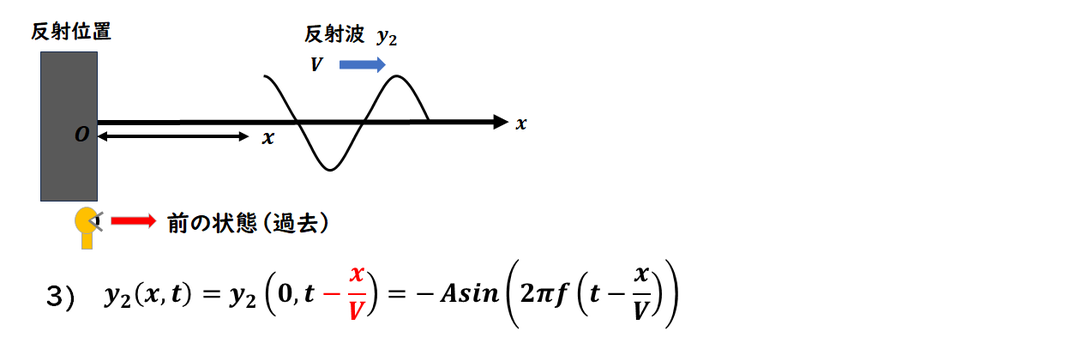
x位置における
反射波の変位を求めます。
反射波は
+x方向 に進む波なので、
通常の進行波と同じ形で
式を立てられます。
波は 過去の位置から
現在へ伝わる ため、
時間の表現は
「t-x/V」
となります。
この符号(+か−か)の意味を、
今一度丁寧に確認しておきましょう。
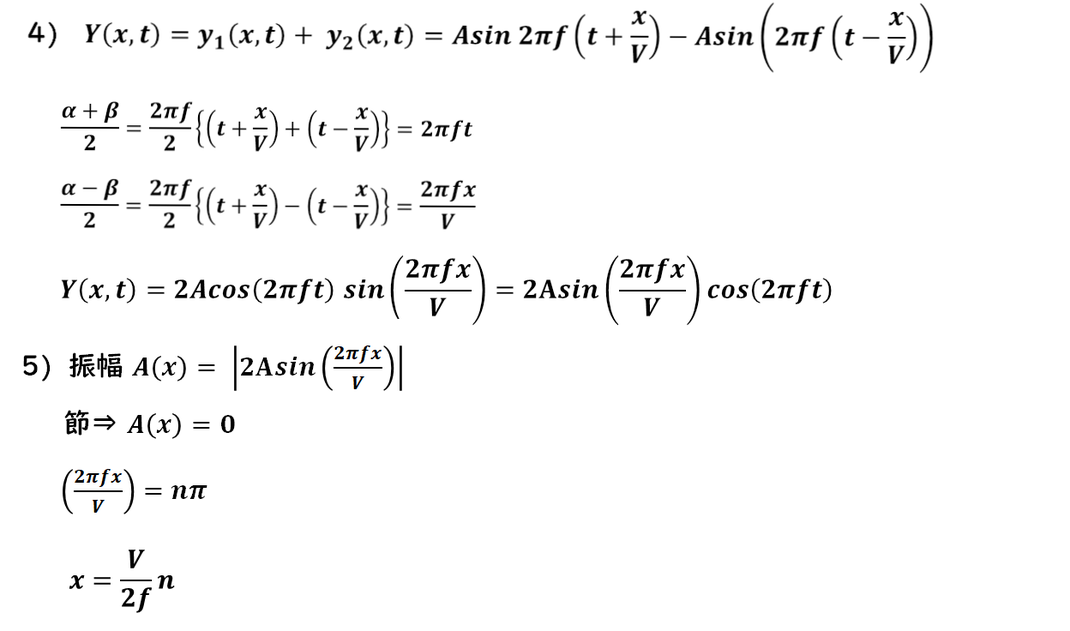
4),5)
入射波と反射波が求まったので、
次に 合成波を計算 します。
間違えずに丁寧に計算
できるようにしましょう。
合成波から 振幅を求め、
そこから 節の位置 を計算します。
このとき、
節の条件が「振幅 = 0」
であることに注意してください。
具体的には、
合成された振幅に現れる
sin の項が 0 になる条件、
sin(nπ) = 0 (n は整数)
となる点が
節の位置 になります。
