直流回路
演習解説
a.c.e.は標準的な問題です。
b.d.f.はやや難しい問題になりますが、
直流回路の解き方を基礎からしっかり身につけていきましょう。
キルヒホッフの法則や、コンデンサにおける電荷保存則を
正しく立てられることが重要です。
また、解答にはいくつか数学的な処理も出てきます。
ですが、これらは入試でもよく出題される内容ですので、
もし初めて見るものがあっても大丈夫です。
一緒に数学の分野としても演習を重ねていきましょう。
一歩ずつ確実に取り組めば、必ず力がついていきますよ。
a. 1)
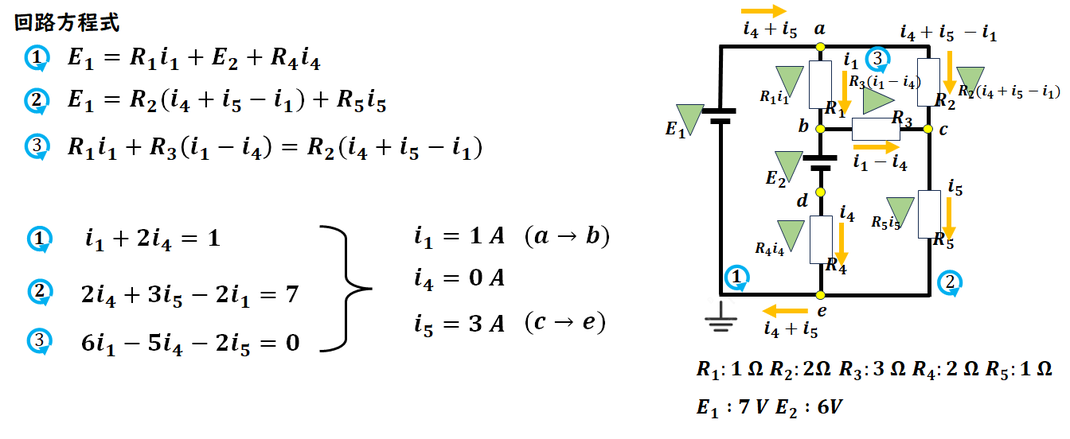
求める電流を、R1・R4・R5 の電流を
それぞれi1,i4,i5 とします。
電流の向きについては、どちらか一方に決めればよく、
もし逆に仮定した場合は、負の値として求まります。
キルヒホッフの第一法則より、
R2・R3 を通る電流は i1,i4,i5 を用いて表すことができます。
次に電流の向きと大きさを設定できたので、
回路方程式を立てます。
与えられた R, E の値を代入して式を整理すると、
3つの方程式が得られます。
未知数は3個(i1,i4,i5)、式も3本あるので、
解くことが可能になり、
それぞれの電流を求めることができます。
今回は、すべて正量で求まったので、
このままの向きで、解答します。
2)
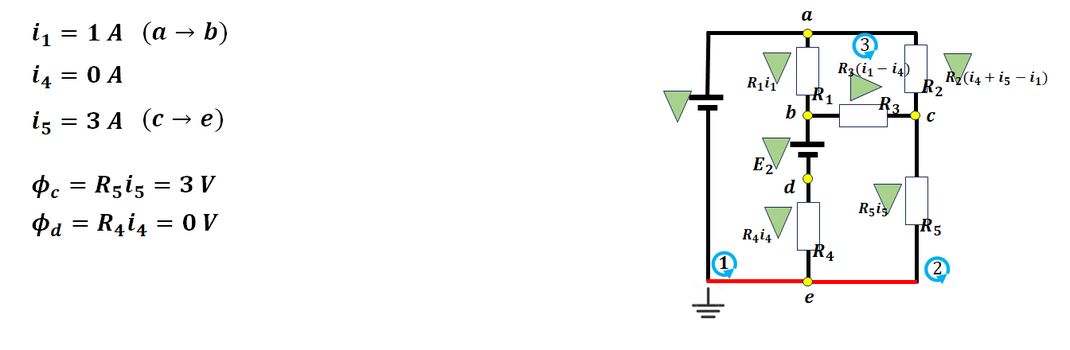
各素子の電圧は求まったので、
c・d点電位を計算します。
e位置が0Vより、
電位を計算していきます。
赤線部はどこも0なので、
Φc = R5i5
Φd = R4i4
で求まります。
3)
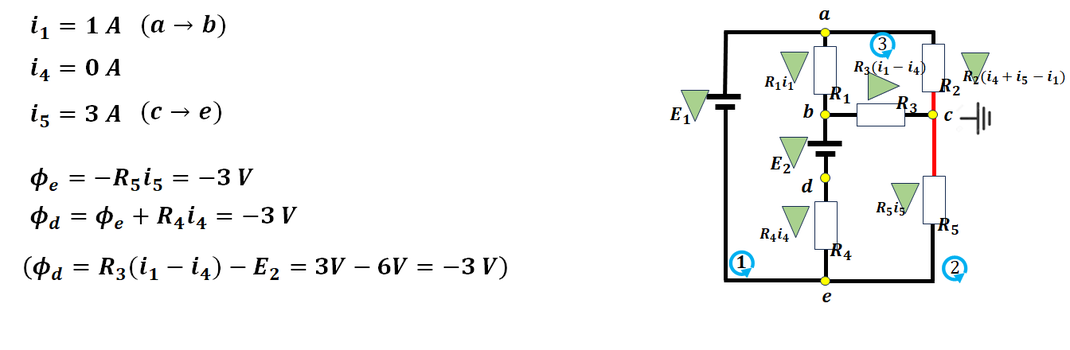
電位0の位置がcに変更になります。
素子の電圧は同じなので、
電位を求めます。
どのように求めて
いっても同じになります。
b.
[1]

回路方程式と第一法則を正しく
立てられるようにしましょう。
物理としてはここで一段落となり、
この先は数学的に電流を計算していくことになります。
回路方程式と第一法則さえ
正しく立てられていれば、心配はいりません。
もしここから電流をうまく求められなかった場合は、
「何を求めるべきなのか」を改めて確認し、求める順序を整理してから
計算に取り組むとよいでしょう。
焦らず順序を大切に進めていけば、必ず解けるようになります。
以下は、解答例となります。
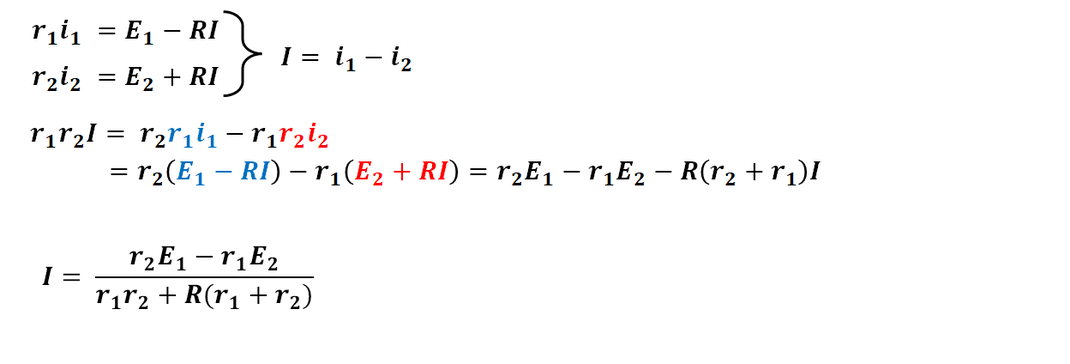
2)

ジュール熱はRi^2,
仕事率は 電源の電圧 × 電源に流れる電流 になります。
それぞれを計算し、
和をとることで両者が一致することを確認しましょう。
以下に解答例を示します。
なお、仕事率から計算してジュール熱の和に
たどり着く方法でも構いません。
どちらの方法でも、
原理がきちんと一致することを体感することが大切です。
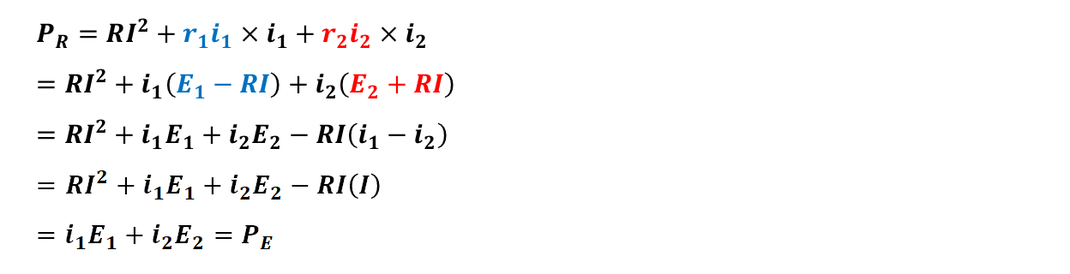
3)
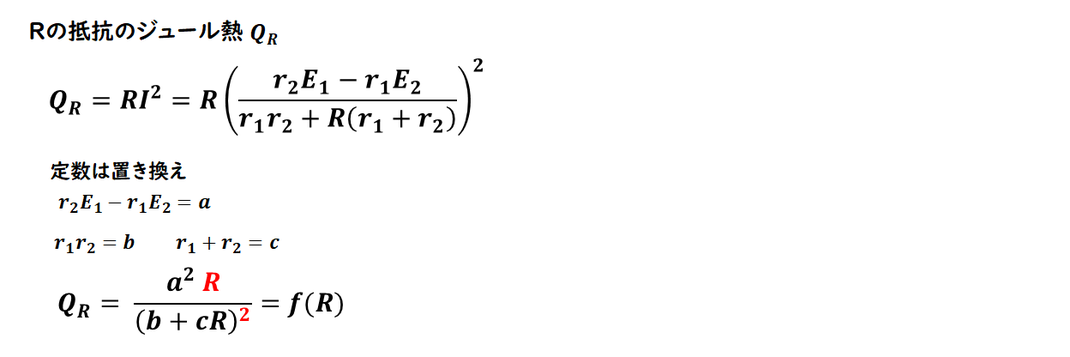
最大となる R を求める問題です。
式が複雑なので、
まずは 定数を置き換えて整理 しましょう。
すると、分数の関数になります。
ここで、
式を見ても「どう処理すればいいのかピンとこない」場合は、
微分して最大値となる R を求めるのが基本です。
一方で、微分を使わない場合もあります。
分数型の関数の問題では頻出で、
相加相乗平均を利用する方法が有効です。
以下は、相加相乗平均を利用して最大値となるRを計算します。
相加相乗平均をまったく聞いたことない場合は
数学の項目あるので、参照してください。

ここでは、やや「無理やりな変形」に
感じるかもしれませんが、
式を整理すると
青で示した項が現れ、その積が定数 になります。
このような形になったら、
相加相乗平均を利用できるのがポイントです。

物理の問題では、相加相乗平均を利用する
ケースがかなり頻繁に出てきます。
特に入試問題では、
暗黙のルールとして
微積分を使わない方向で解かせる ことが多いです。
そこで、分数の式になり、分子が定数でない場合には、
「一度分子を無理やり定数に変形できないか」考えてみましょう。
もし形を整えられれば、
相加相乗平均を適用できるかどうかが見えてきます。
注意点としては、
不等号の向きを忘れてしまうことがよくあります。
そんなときは、 (a-b)² ≥ 0 という
当たり前の事実を思い出し、
変形してみると、
不等号の向きが自然に確認できます。
[2]
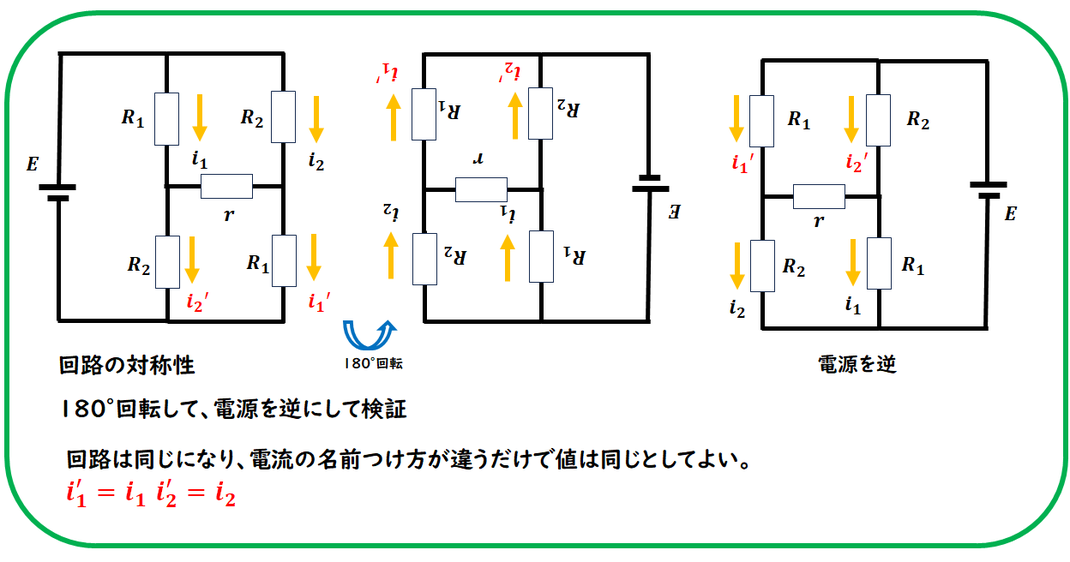
この問題も、
回路方程式とキルヒホッフの第一法則を使って解答していきます。
ただし、実際に電流を全部立てると、
電流の数が5個にもなり、計算がかなり複雑になってしまいます。
そこで、
このように同じ抵抗値が複数登場する場合は、
ぜひ 回路の対称性 を検討してみてください。
回路の対称性にはいくつかの考え方がありますが、
まず試してほしいのは、
回路を180°回転させて電源を逆にしてみる方法です。
すると、回路の形が元と同じになり、
対応する電流が同じ値になることを確認できます。
この工夫によって、
立てる式の数をぐっと減らすことができ、計算が楽になります。
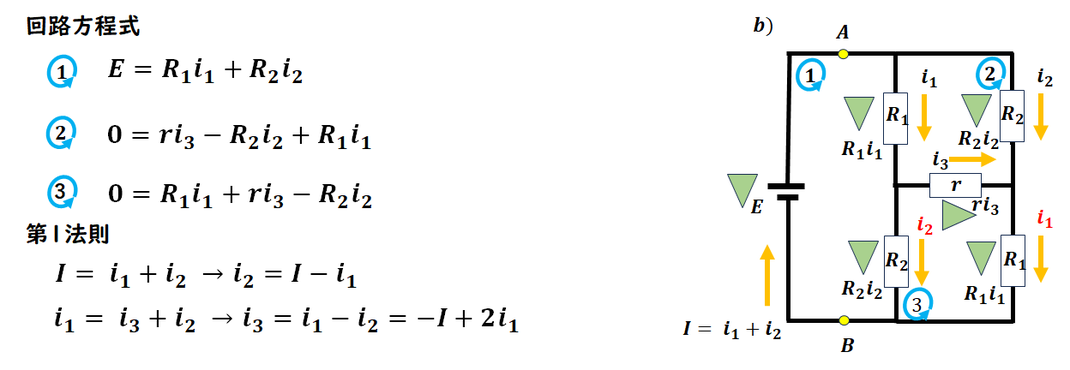
対称性を利用すると立式の数を減らすことができました。
ただし、気をつけてほしいのは、
「同じ抵抗だから同じ電流が流れるだろう」と勝手に決めつけないことです。
対称性に気づいたら、
実際に図を描いて本当に同じ回路になるか検証することが大切です。
これを確認してはじめて、
「この抵抗には同じ電流が流れる」と安心して使えるようになります。
後は計算なので、解答例は以下になります。
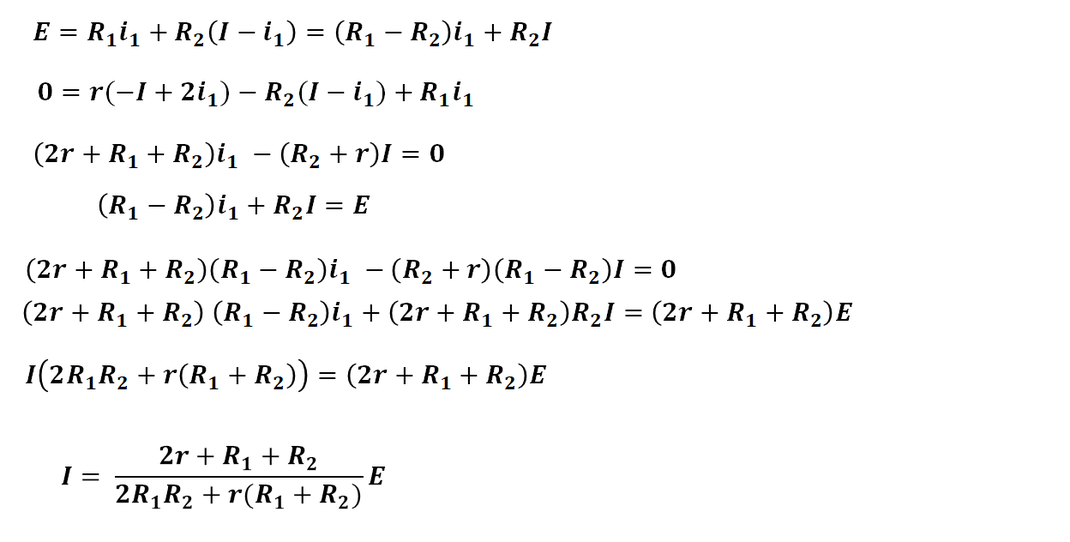
5)
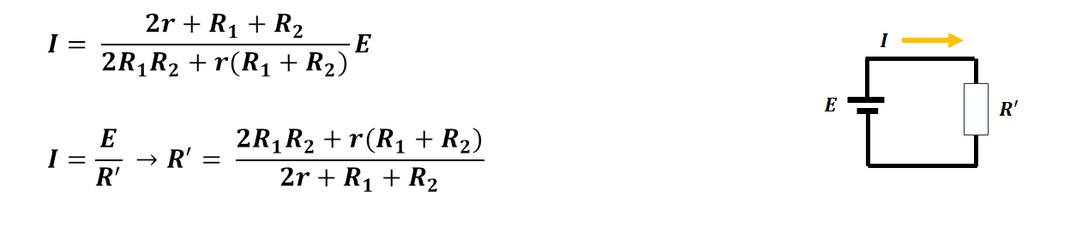
電源を流れる電流がわかったので、
合成抵抗を求めることができます。

コンデンサの回路問題では、
・回路方程式をたてる。
・電荷保存則をたてる。
をまず、しましょう。
電荷保存則は、接続部があれば
その場所を利用していきましょう。
各回路毎解答していきます。
1)
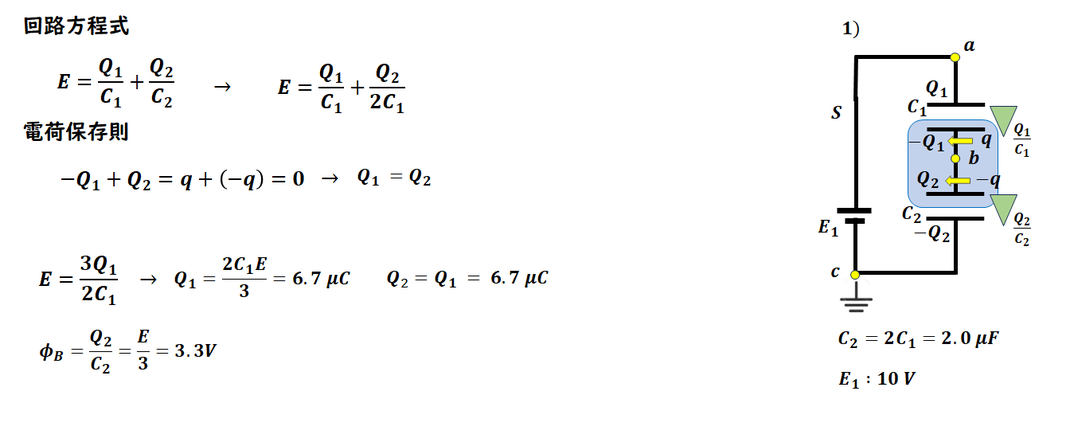
コンデンサの電荷を設定し、
回路方程式、電荷保存則を作り
解答します。
電荷保存則は、常に0ではなく、
最初の電荷量になることに
気を付けてください。
2)
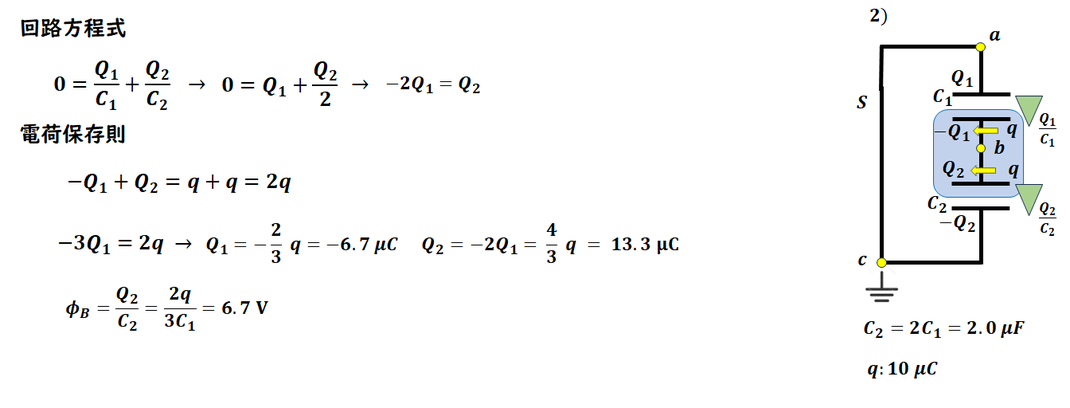
3)
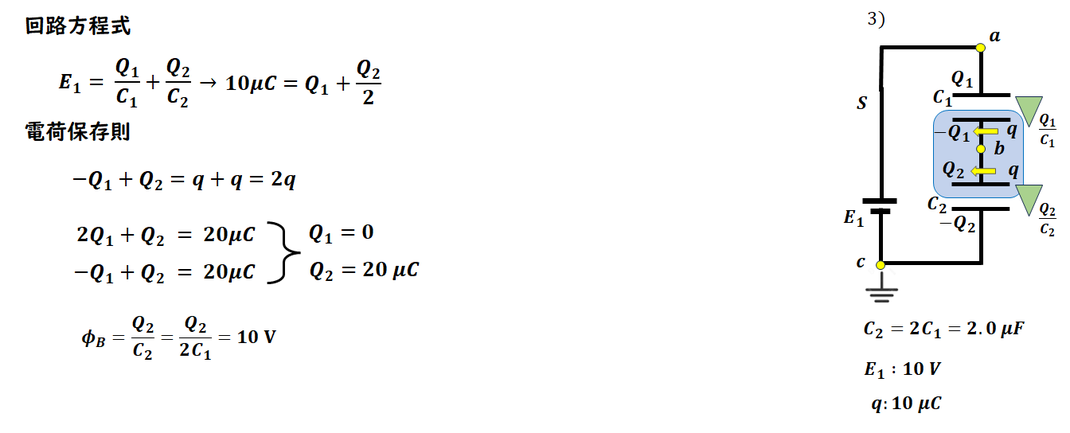
4)
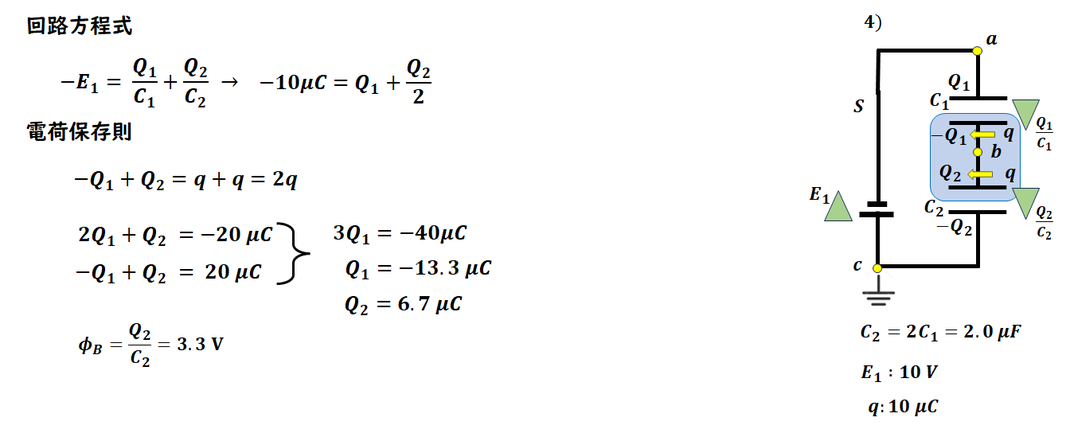

コンデンサの回路問題では、
・回路方程式をたてる。
・電荷保存則をたてる。
をまず、しましょう。
d.
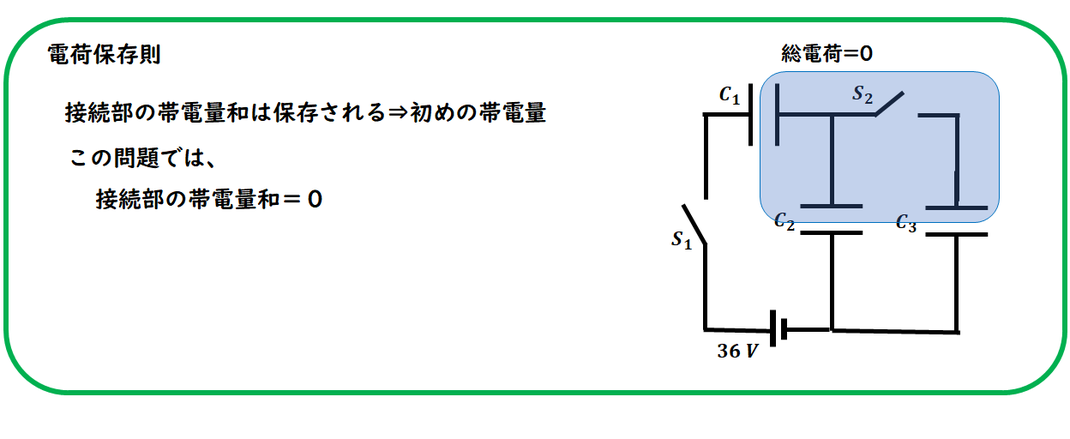
この問題では、上図の「島(節点)」において総電荷=0
であることに気づくのがポイントです。
スイッチが含まれているので少し見落としやすいですが、
電荷保存則はスイッチの有無にかかわらず必ず成り立ちます。
さらに、このタイプの「無限にスイッチがある回路」では、
漸化式を立てて考えることになります。
もし漸化式の扱いに不安がある人は、
この機会にもう一度しっかり確認しておくとよいでしょう。
1)
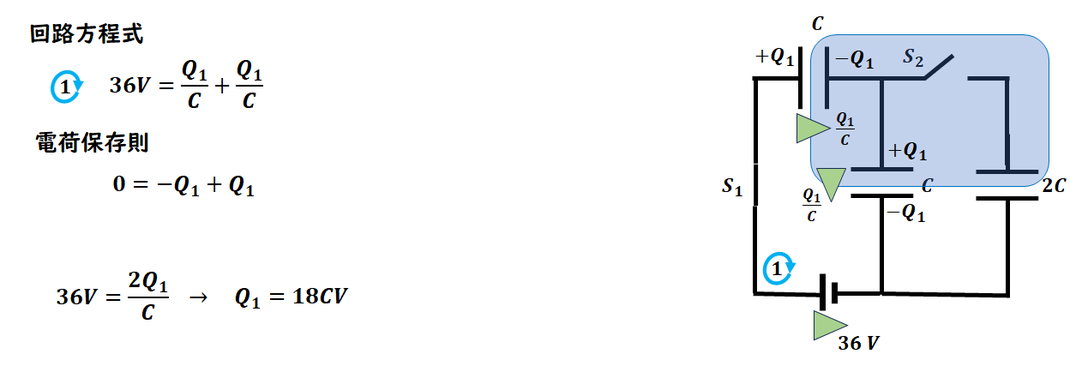
電荷を設定して、
回路方程式と電荷保存則を作ります。
電荷が同じとあるので、
電荷保存則を忘れても解けてしまいます。
2)
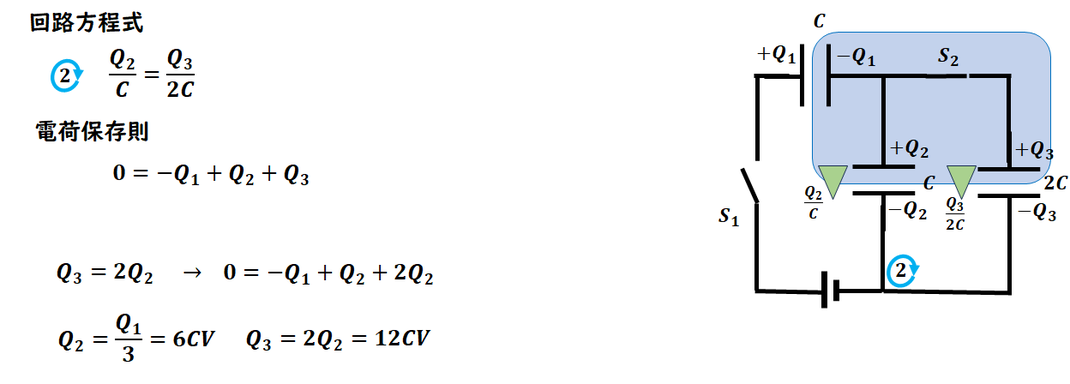
電荷を設定して、
回路方程式、電荷保存則をたてます。
計算して電荷を求めます。
ここまでが1回目の操作です。
3)
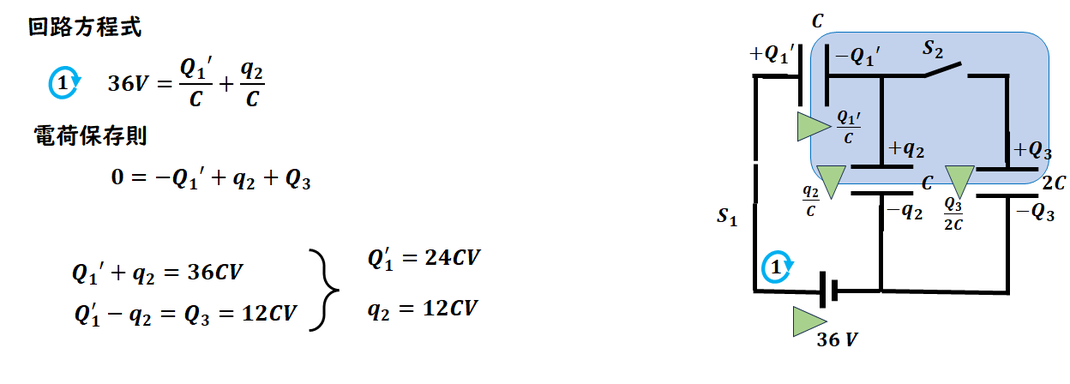
2回目の操作 になります。
同じように、回路方程式と電荷保存則を立てて考えていきましょう。
ここでは、
コンデンサー C2 に蓄えられる電荷をq2 としています。
最終的な値(Q2)とは区別するためにこうしていますが、
もちろんQ2 としてしまっても構いません。
こうした整理をしておくと、
あとで漸化式を立てるときにスムーズに進められますよ。
また、電荷保存則は「直前の値」ではなく、
常に「初期値」から考える方が計算が楽になることが多いです。
この問題では、
初期値を常に 0 として扱ってよいので、その点も意識してみてください。
4)
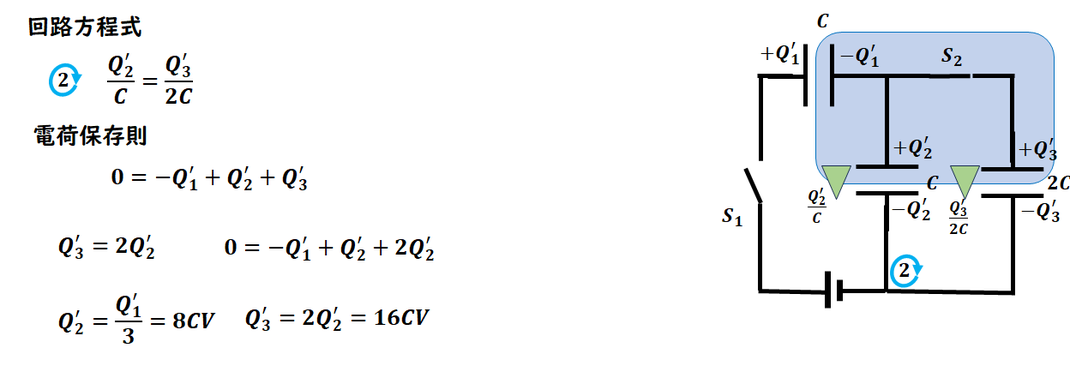
2回目後半です。
Q2は正規のQ2として
同様に、
回路方程式、電荷保存則をたてます。
ここで、2回目終了です。
5)
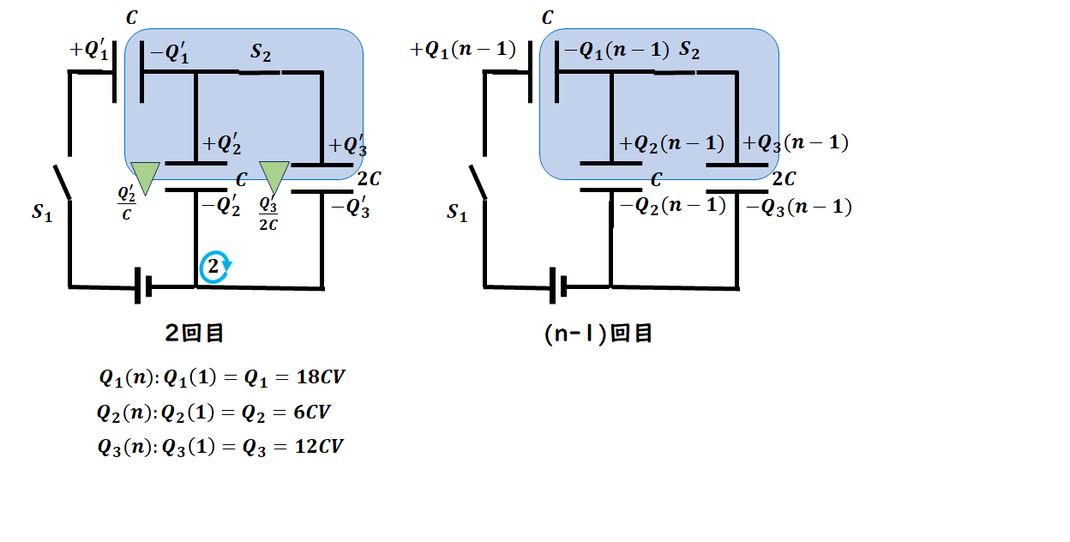
この問題では
「n−2回スイッチ操作をした後の状態」となっているので、
実際には「すでに2回操作した後、n回目の電荷を求めなさい」
という意味になります。
では、どうすればよいか?
基本は (n−1)回目の状況を仮定して、
その次の n回目の電荷を求める という手順になります。
(言い換えれば、n回目 ⇒ (n+1)回目 の関係式を立てる、ということです。)
実際の計算に入る前に、
まずは (n−1)回目の電荷の状況を整理しておくとスムーズです。
例えば、数列のように
Q3nとしても良いです
と添字をつけて表す方法もありますし、
ここではシンプルに Q3(n) を添える書き方にしています。
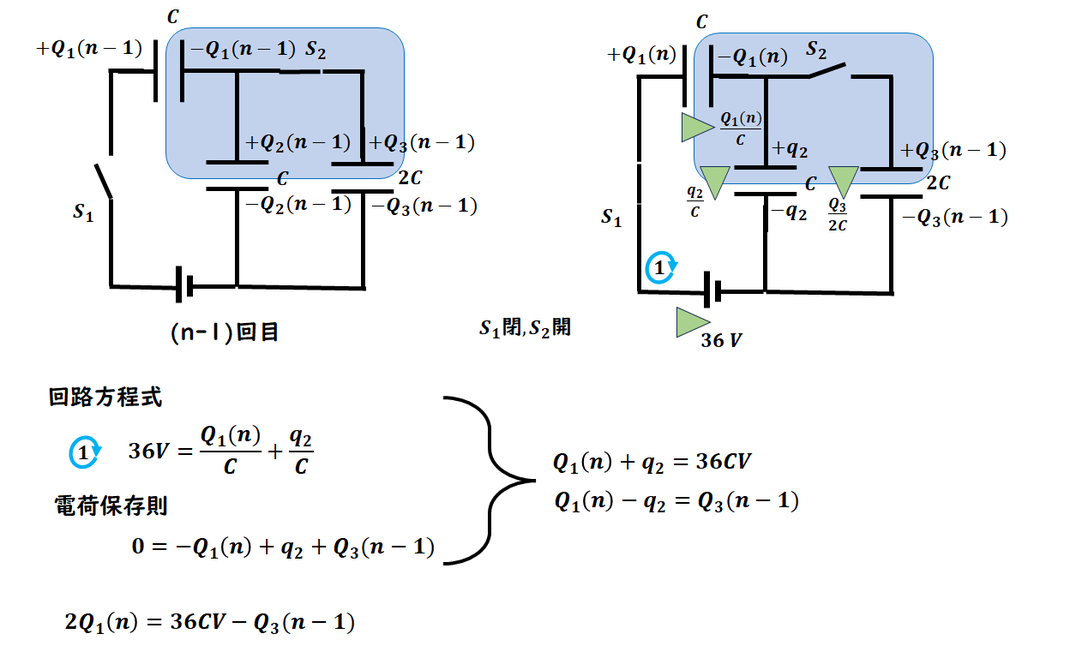
電荷を設定したので、
実際に操作を行います。
まず前半です。
同様に、
回路方程式、電荷保存則をたてて、
Q1を求めます。
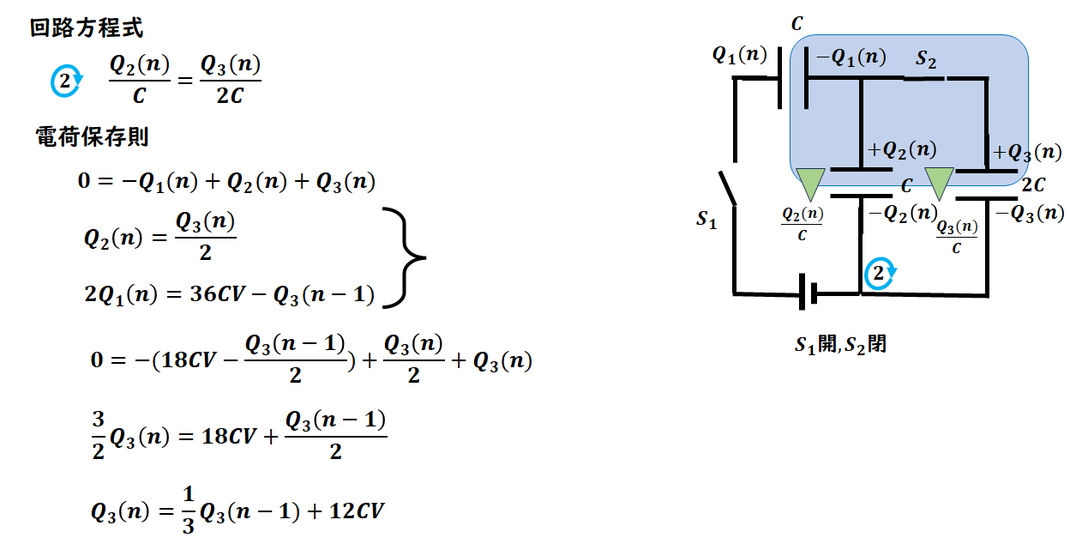

後半です。
同様に、
回路方程式と電荷保存則を立てます。
今回求めるのは C3 の電荷なので、
途中で現れる Q1,Q2 を消去していく計算になります。
この手順を進めると、Q3 の漸化式が得られます。
したがって、この漸化式を解くことが目標です。
この漸化式は解けますか。
解けない場合は、
いちど参考書で漸化式の解法を確認してから取り組んでください。

この漸化式を解ける人は
少なくないと思いますが、
「公式として一般解を覚えている人」は
意外と少ないのではないでしょうか。
この2項間漸化式は、
確率分野や他の漸化式の問題でも頻出です。
そのため、
基本的には一般解を覚えておく方が有利だと思います。
上位層の受験生は、
すでに公式を覚えていて、数秒で答えを出してしまいます。
もちろん、
αを求めて式を変形し、等比数列に持ち込むことで解けますが、
どうしても数分かかってしまうことが多いです。
ですから、
漸化式の解法が理解できている人ほど、
一般項を公式として覚えてしまうことを強くおすすめします。
本番での時間短縮につながり、得点力アップに直結しますよ。
これを利用して、Q3を求めます。
6)
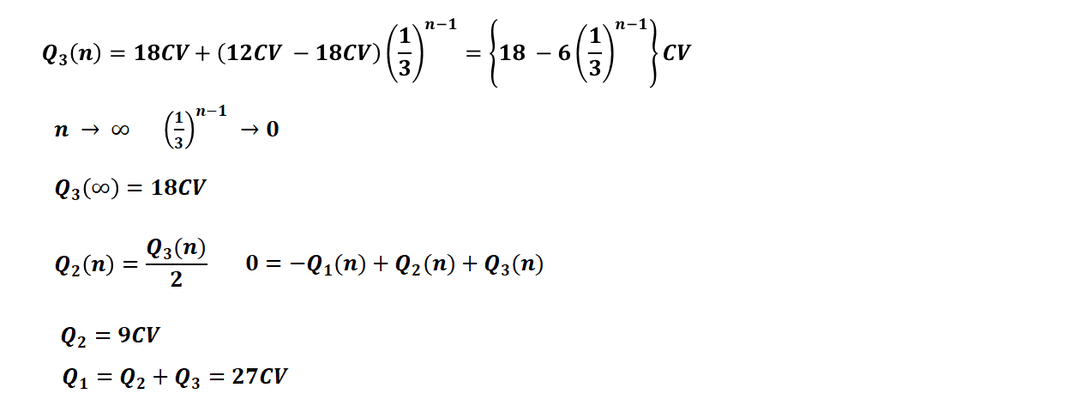
5)ができた人への
ボーナス加点問題です。
最後に仕上げをしてみましょう。
n→∞ とすると、分数項が 0 に近づきます。
したがって、
極限値として Q3 の最終値 を求めることができます。
その後、
Q2,Q1 も自然に求められ、問題は終了です。
e.

コンデンサの過渡現象の問題です。
スイッチを入れた瞬間は、電荷はそのまま。
十分時間が経つと、電流は 0 になります。
この2点をしっかり覚えて解きましょう。
[1]
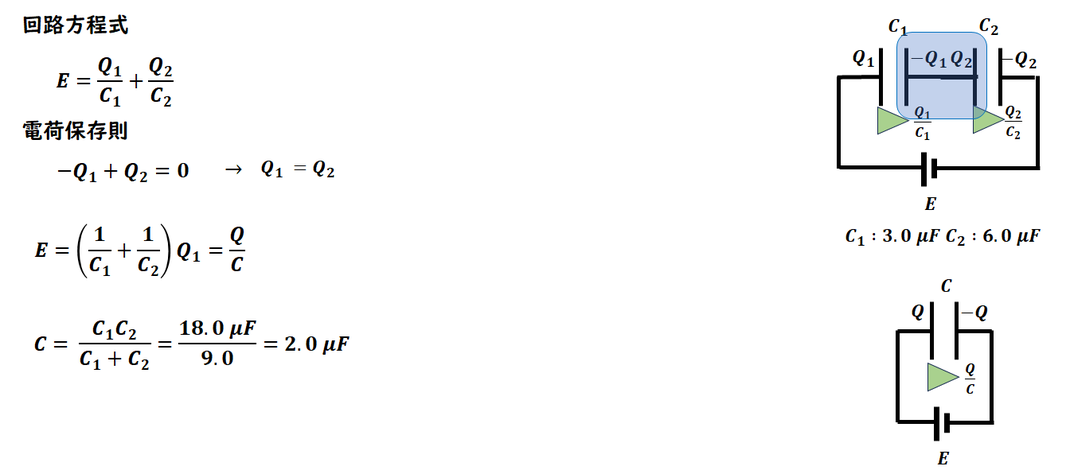
直列の場合のコンデンサの合成容量です。
覚えていれば、そのまま計算できます。
回路方程式と電荷保存則を用いて各電荷を計算し、
1つの素子と仮定して合成容量を比較して求めます。
2)
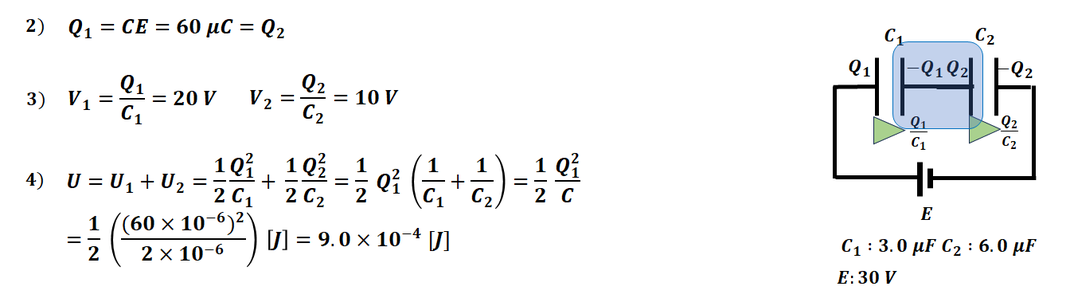
1) で回路方程式、電荷保存則をたてたので
実際の値を代入して計算します。
エネルギーについては、
1素子として求めても同じになります。
3)
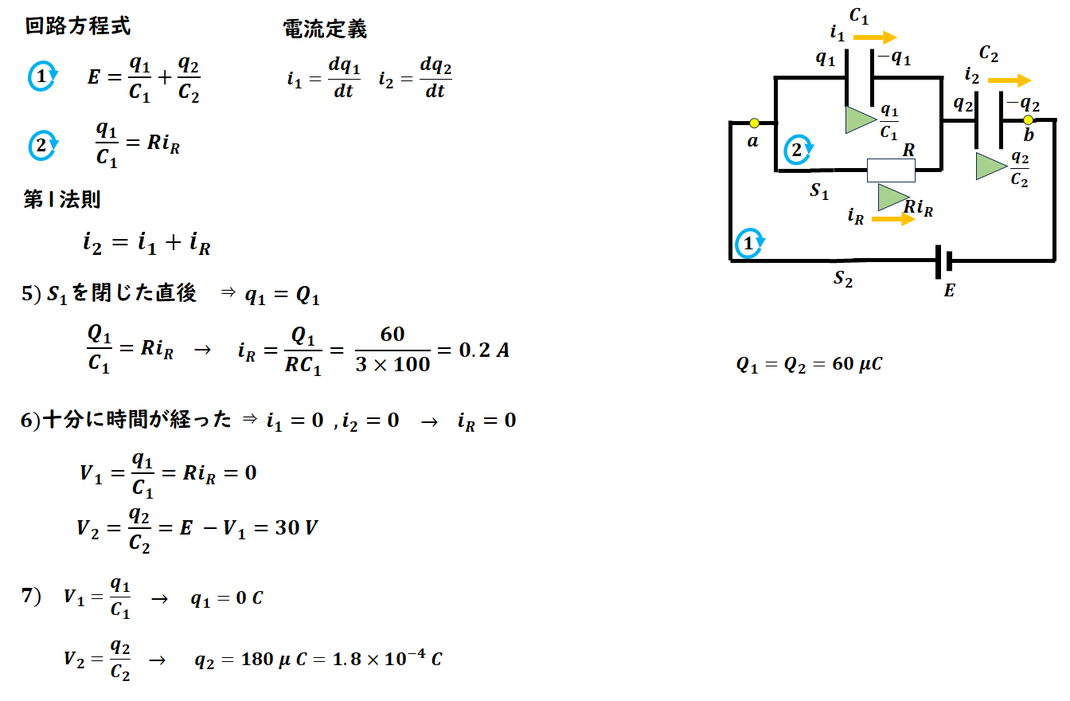
抵抗を含む回路になり、
過渡現象の問題です。
5), 6)ごとに回路方程式や
第一法則を立てて求めても構いません。
ここでは、
電流が流れているときの回路方程式を立てています。
コンデンサは、
スイッチを入れた瞬間は、電荷はそのまま。
十分時間が経つと、電流は 0 になります。
を利用して計算して解答しましょう。
f

コンデンサ、コイルの過渡現象の問題です。
スイッチを入れた時、十分時間が経ったときの
状況をしっかり覚えましょう。
特に、電圧0の時に、電流が0,0でない時があるので
注意し意識的に覚えましょう。
解説は、a) コイルの時 b) コンデンサの時を分けてします。
a) コイルの時
1) ~ 3)
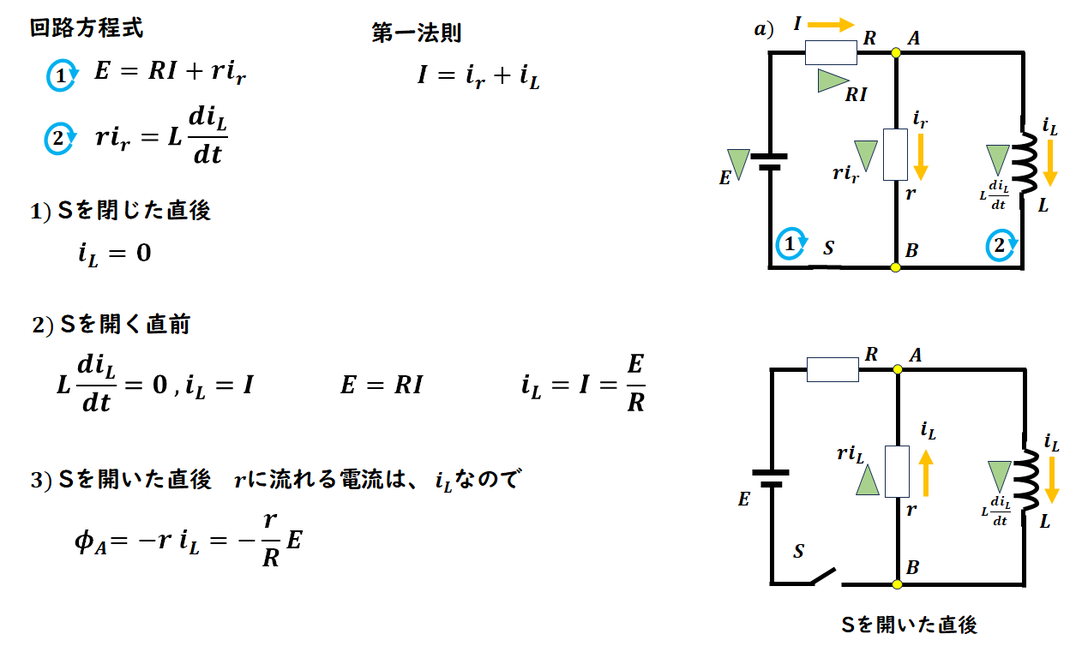
2個の閉回路について
回路方程式、第一法則を作ります。
ここでは、まとめて作成していますが、
設問毎に作っていってもよいです。
1) スイッチを閉じた時のコイルに流れる電流です。
⇒ この時は電流0で断線扱いになります。
2) 十分時間が経った後は、電圧は0ですが、
導線扱いとなり、抵抗側には電流は流れません。
このことから、コイルを流れる電流を計算します。
3) Sを開くと、そのまま電流が抵抗側に流れるので
電位を計算します。
4)
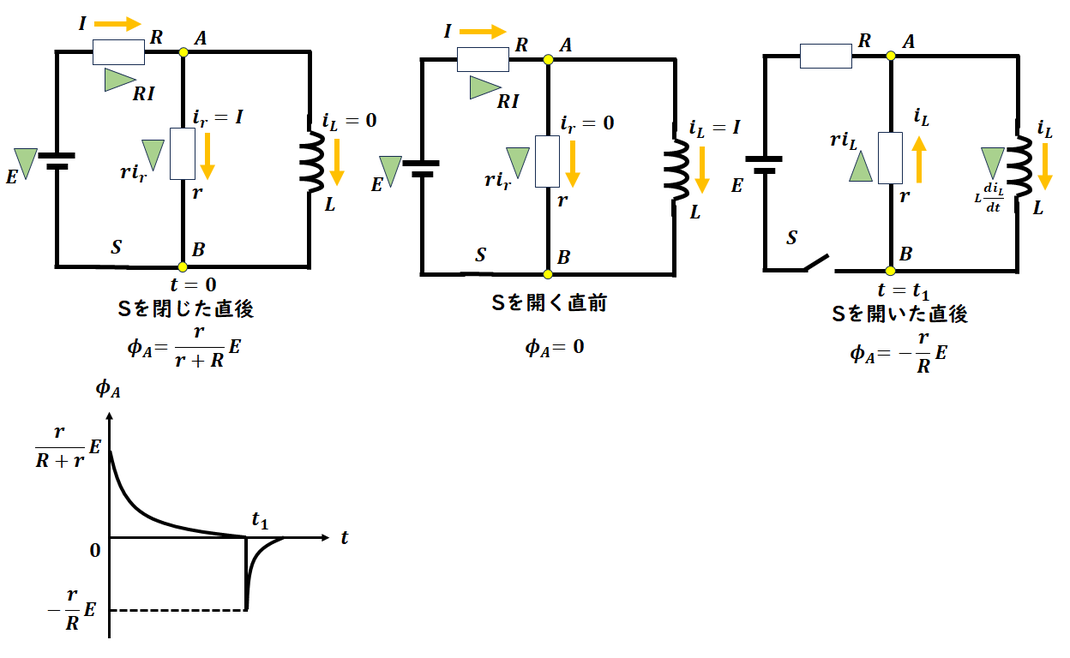
Sを閉じる、十分時間が経つ(Sを開く直前)、
Sを開く状況をまとめて、各状況の電位を計算します。
しっかり電位が求められるようにしましょう。
グラフを描きます。
各状況への推移は、単調減少、増加であれば、
この問題では良いです。
正式には、指数関数になります。
5)

エネルギー保存則で、
コイルのエネルギーをInとします。
最終的に、電圧=0になるので、
コイルのエネルギー=0になります。
この変化分が抵抗のジュール熱に変わることになります。
抵抗のジュール熱=コイルのエネルギー
から解答します。
b) コンデンサ
1) ~ 2)
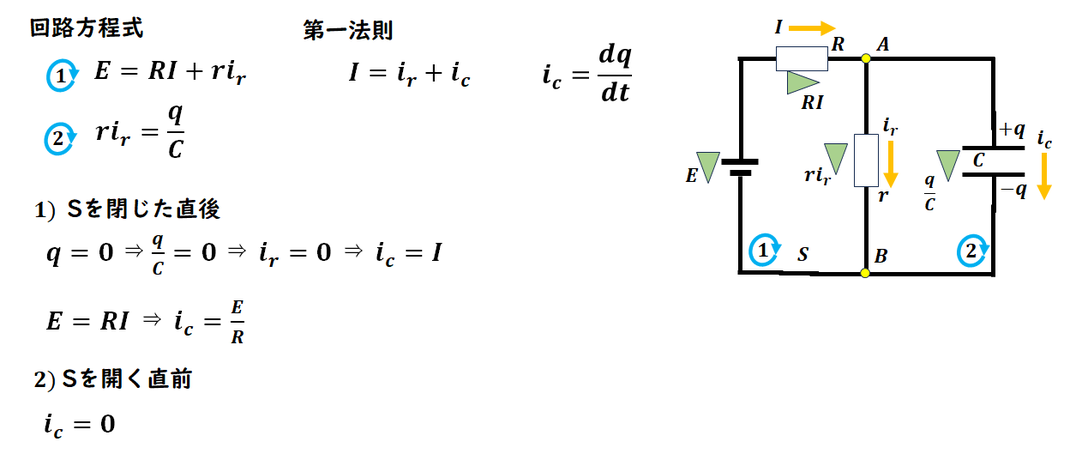
コンデンサの時も
同様に、回路方程式、第一法則をたてます。
1) 電荷が0です。電圧=0より
抵抗に流れる電流=0
したがって、コンデンサに流れる電流は
E-RIより求まります。
直後は、電荷が0(そのまま)、導線扱いを覚えましょう。
2) 十分時間が経ったときは、
コンデンサを流れる電流は0です。
断線扱いになります。
3)

状況を整理して解くことにしましょう。
十分時間が経っているときの
電荷を求めましょう。
コンデンサへの電流は0なので、
回路を流れる電流から、電荷が計算できます。
この状態で、Sを開くと
コンデンサから電流が流れます。
この時の電位は、電荷がそのままなので、
Q1/Cから電位を計算します。
4)
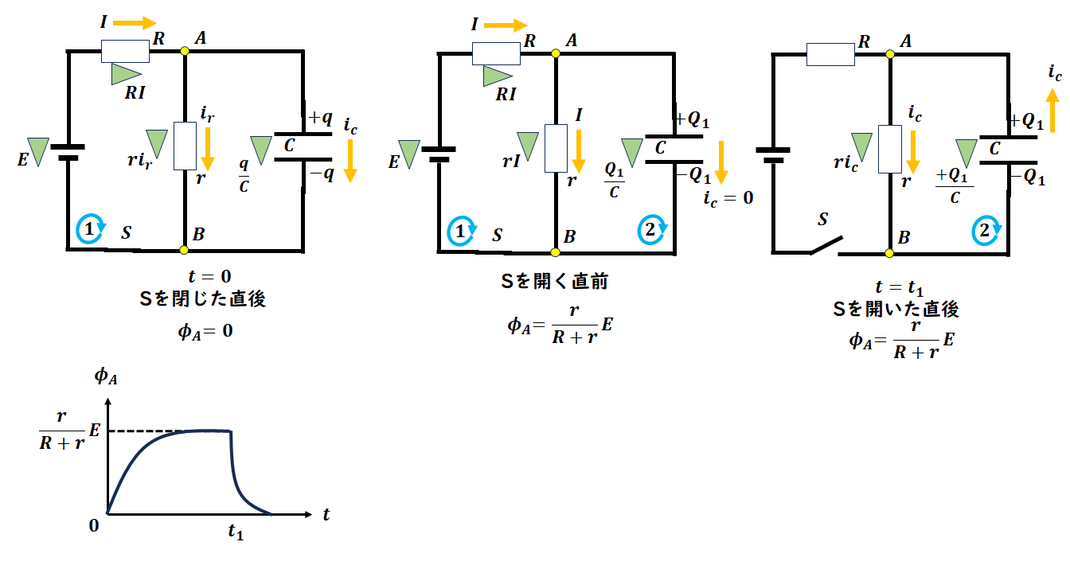
Sを閉じる、十分時間が経つ(Sを開く直前)、
Sを開く状況をまとめて、各状況の電位を計算します。
しっかり電位が求められるようにしましょう。
グラフを描きます。
各状況への推移は、単調減少、増加であれば、
この問題では良いです。
最後Sを開いた後、コンデンサは放電します。
その後、電荷はなくなっていき最後電位は0になります。
正式には、この時も指数関数になります。
5)
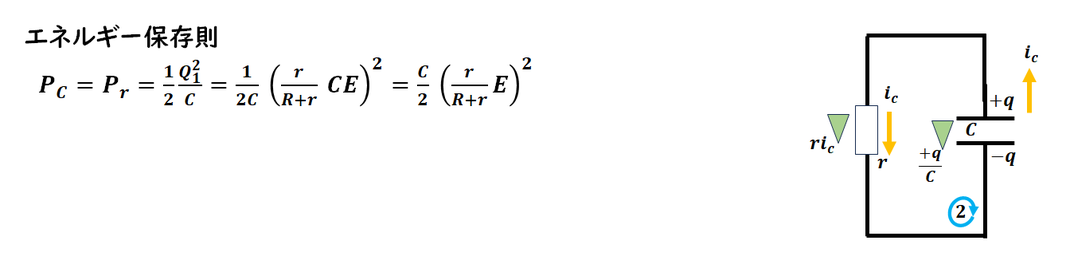
コイルの時と同様で、
エネルギーInはコンデンサになります。
最後放電してエネルギーは0になります。
この変化分が抵抗のジュール熱に変わることになります。
抵抗のジュール熱=コンデンサのエネルギー
から解答します。
時間変位
変位の時間変化が
指数関数になることを導出します。
以下の計算手順は、おぼえても大きな
アドバンテージにはなりません。
余力があれば、
実際に手を動かして
計算してみて計算方法を実体験してください。

時間変位が指数関数になることに
納得がいかない方もいると思います。
回路方程式から電位を計算することで、
指数関数を導けます。参考にしてみてください。
求め方はどのようでも構いませんが、
ここではコイルを流れる電流を例にしています。
途中で微分方程式が現れます。
「微分すると自分自身の倍数(±自分)」
になる関数は指数関数なので、
その解は必然的に指数関数となります。
なお、
この形は力学における空気抵抗を受ける運動でも同様に現れます。

コンデンサの場合も同様に
回路方程式から計算でき、
指数関数になります。
t1以降も解くことはできるので、
計算してみてもよいかと思います。
・直流演習問題
