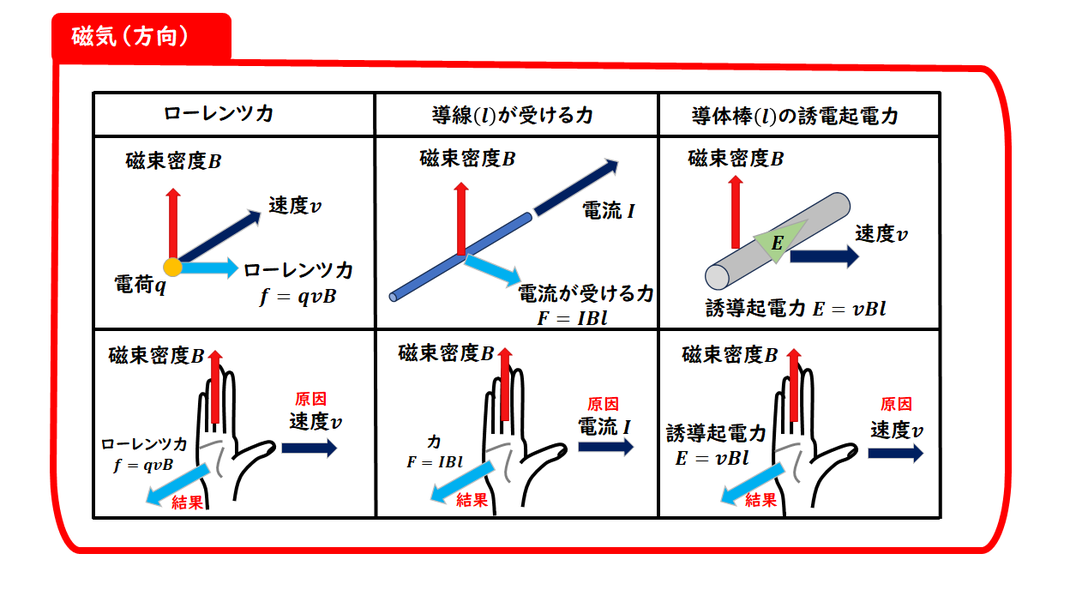
電磁誘導の説明です。
よく出題されるので
向きなどを間違えないように
演習しましょう。
1.磁界の向き
■磁界中で働く力の向きについて
磁界で力の向きを扱う際には、
右手を使った覚え方があります。
-
親指:原因(速度や電流の向き)
-
他の4本の指:磁場の向き(磁束密度B)
-
手のひら:結果(力や誘導起電力の向き)
ただし、ローレンツ力の場合、
電荷が負(電子など)である場合は、
手の甲の方向が力の向きになります。
磁界に関する問題では「向き」が非常に重要です。
自分が間違えにくい方法で
しっかりと覚えましょう。
なお、
フレミングの左手の法則で
覚えている場合は、
特に変更の必要はありません。
補足:
磁束密度(B)が運動や
電流の方向に対して
垂直でない場合は、
その垂直成分(B⊥)を
用いて力の大きさを求めましょう。
2.電磁誘導(ファラデーの法則)
■ファラデーの法則と
誘導起電力の求め方
ファラデーの法則を使うことで、
誘導起電力V を求めることができます。
この公式を使うには、
磁束の時間変化を求める必要があります。
■ 符号「−」の意味
式の負号は、レンツの法則に対応しています。
つまり、
「磁束の変化を妨げる方向に起電力が生じる」
ことを意味しています。
■ 磁束の定義
磁束は、磁束密度×面積になります。
■ 学習のポイント
ファラデーの法則の式は、
直感的に理解しにくい部分もあります。
そのため、
実際の問題演習を通して
理解を深めていくことが大切です。
導体棒の誘電起動力
■ファラデーの法則の具体例:
導体棒の誘導起電力
ファラデーの法則の代表的な応用例として、
導体棒を使った電磁誘導の問題があります。
このタイプの問題は、
入試や定期試験で頻繁に出題される
重要なテーマです。
・導体棒が磁束密度 B
・一定の速さ vで移動
⇒ 棒の両端には誘導起電力V
ファラデーの法則を利用して
誘導起電力を求めるためには、
磁束の時間変化(磁束の増減)を計算する
必要があります。
時間 Δt 秒後の
磁束の変化量ΔΦ を求めます。
導体棒が長さl、速さv で動くとき、
棒が移動する距離は vΔt です。
ΔΦ = B×面積 = B(lvΔt)
ΔΦ = vBΔt l
磁束変化を求める際、
「S を全体の面積として計算する」
方法もありますが、
複数の導体棒が関与するような
複雑な問題では混乱しやすくなります。
導体棒の移動によって掃かれる面積から
磁束変化を直接計算する方が
確実で、ミスが起こりにくくなります。
ΔΦ = vBΔt l
ファラデーの法則を利用すると、
誘導起電力V
V = ― vBl
ここで、
マイナス符号はレンツの法則によるもので、
磁束の変化を妨げる向きを表します。
反時計回りを正と定義した場合、
符号がマイナスであることから、
誘導電流の向きは時計回りになります。
また、右手を使った方向とも一致するため、
直観的にも確認できます。
このあとの問題では、
導体棒が誘導する起電力を電池とみなして、
回路全体の問題として考えます。
オームの法則:
V = RIより
I = V/R
で求まります。