単振動標準
問題解説
単振動標準演習の解説です。
すべて、必須問題です。
解説では、普通解法と、
パターンを利用した解答も解説します。
常に一般解を解く方法でも良いです。
それほど変わりはなので
得意な方法をとってください。
a.
b.
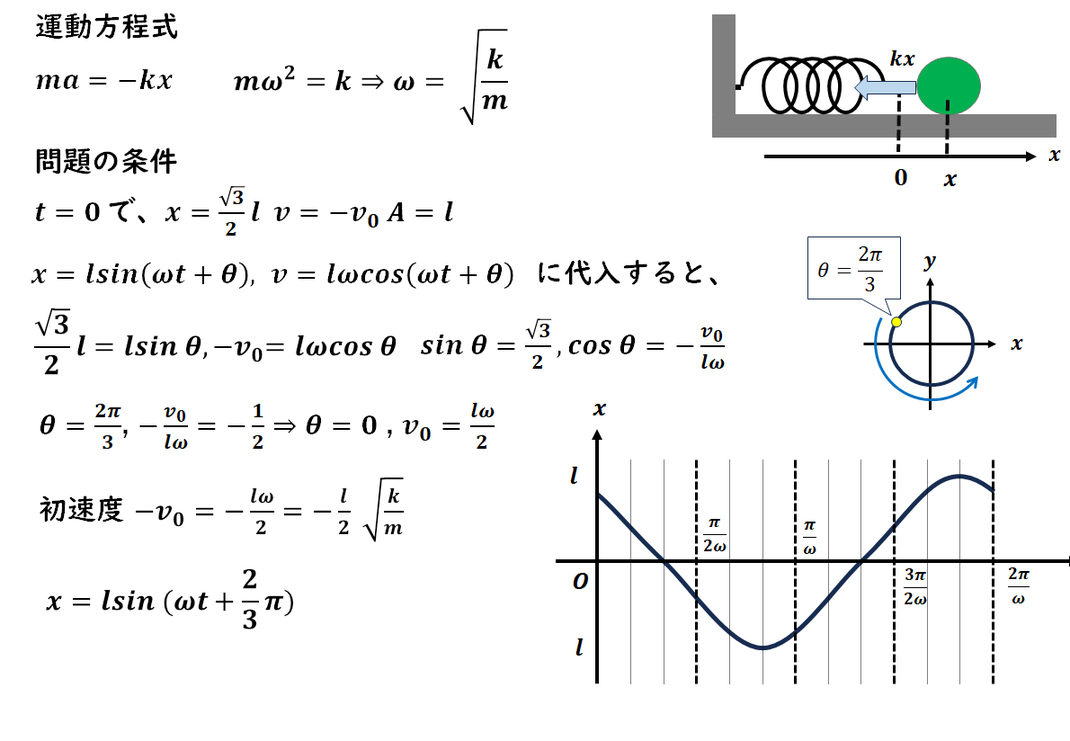
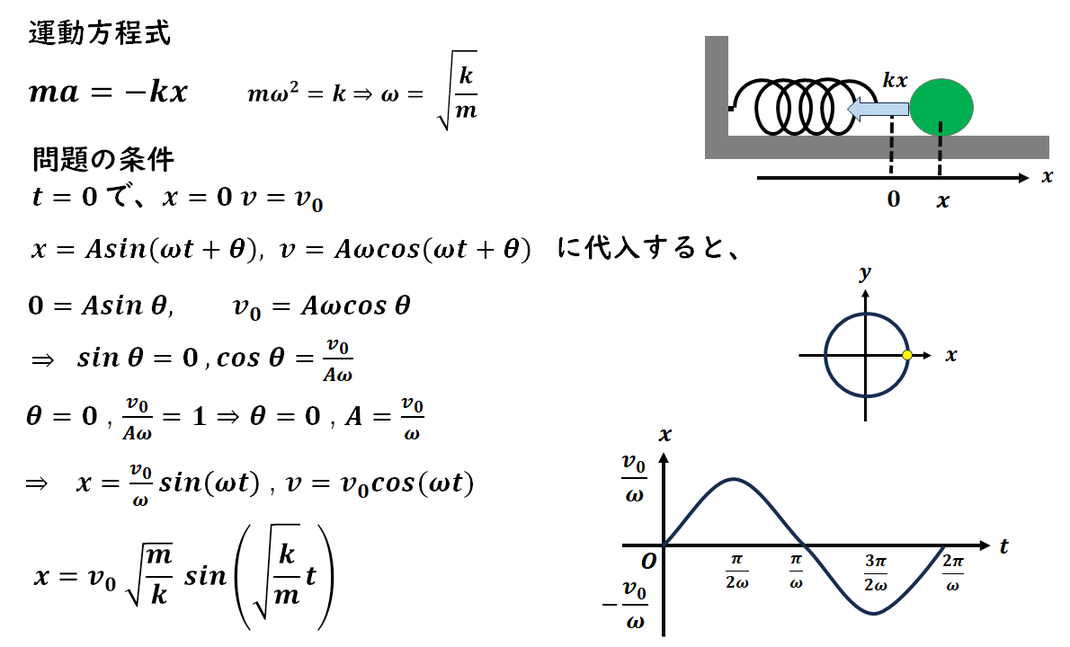
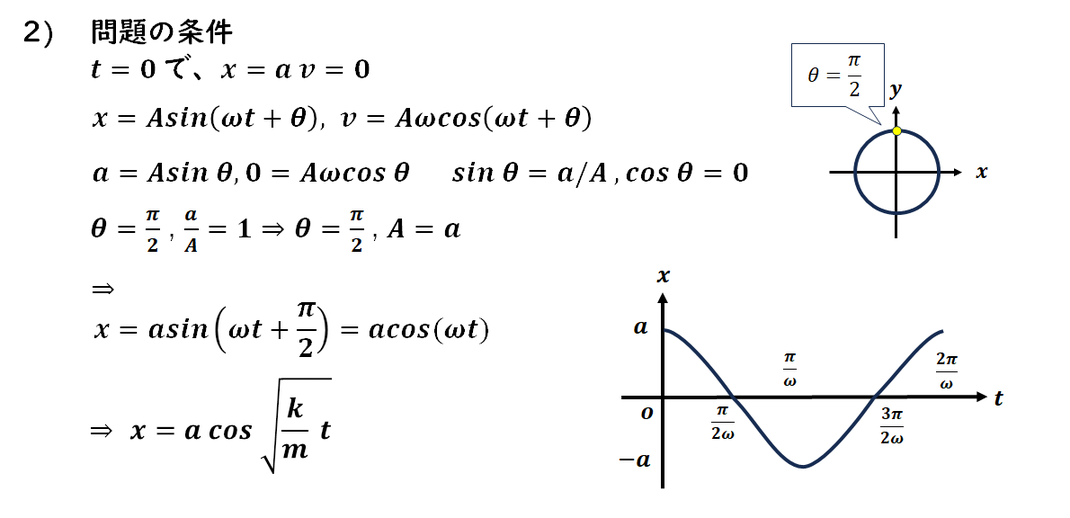
一般解を用いて、
位置と速度の時間変化を式で表し、
グラフにします。
このとき、
初期条件から求まる角度(初期位相)は、
角度が0、π/2、π
といった単純な値にはならず、
位相が2π/3 進んでいることになります。
c. [1]
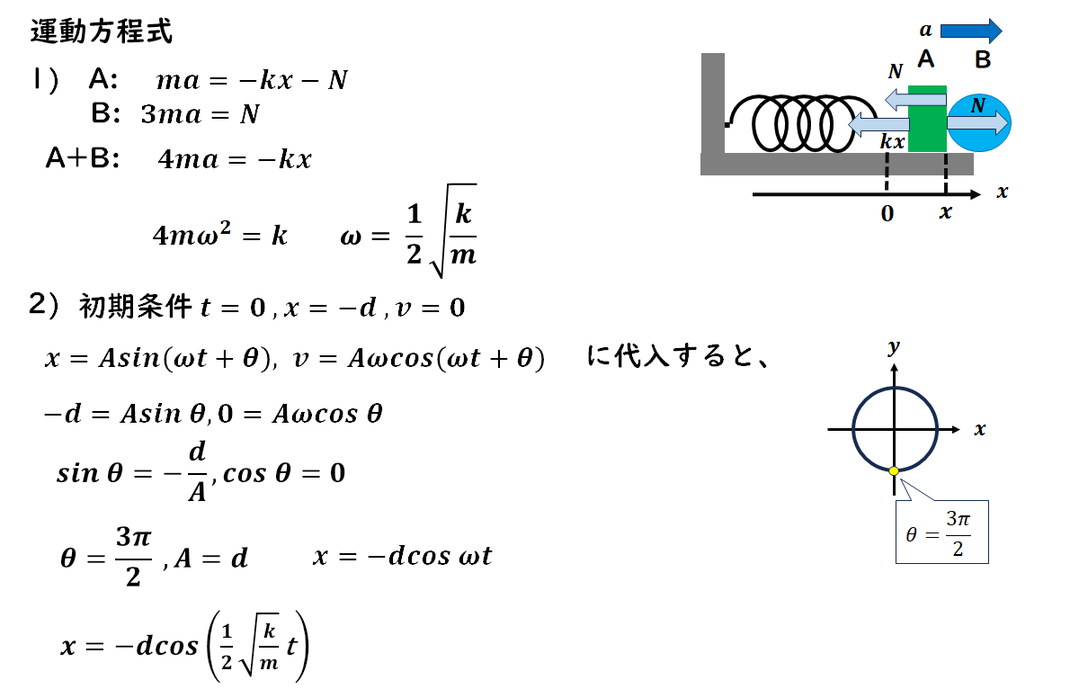
A、B それぞれについて
運動方程式を立てましょう。
今回は問題として指定されていますが、
ふだんから面倒くさがらずに、
必ず個別に立てることが大切です。
問題の状況は x<0 ですが、
負の位置で式を立てると符号の取り扱いがややこしくなります。
そのため、
必ず 正の位置(x>0) での運動として、
運動方程式を立てるようにしましょう。
垂直抗力は作用・反作用で打ち消し合うので、
2つの式を足し合わせると、単振動の式が得られます。
一般解、初期条件から
位置の関数を求めます。

単振動の式をもとに、
各設問に解答していきます。
3) x=-1/2となるときの時間を求めます。
4) Bが離れる条件は、垂直抗力N=0
⇒x=0 となるときの時間を求めます。
5)設問 4) のときの速度を求めます。
速度の式は、振幅A,初期位相θが求まっているため
速度の一般解の式に代入して求めることができます。
また、位置xを微分して速度を求めることも可能です。
いずれにしても、vの時間の式から
速度を計算します。
[2]
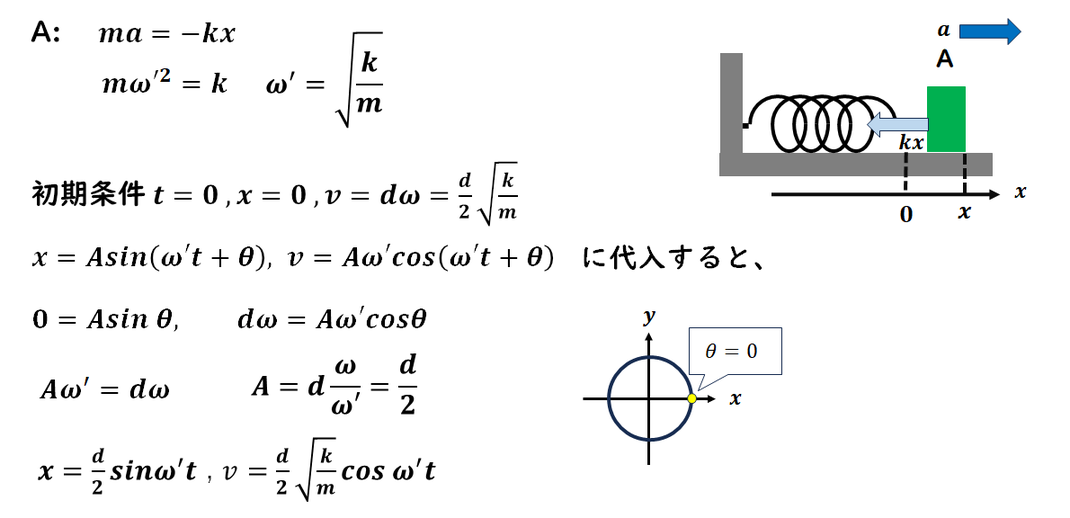
A のみについて運動方程式を立て、
そこから単振動の式を導きましょう。
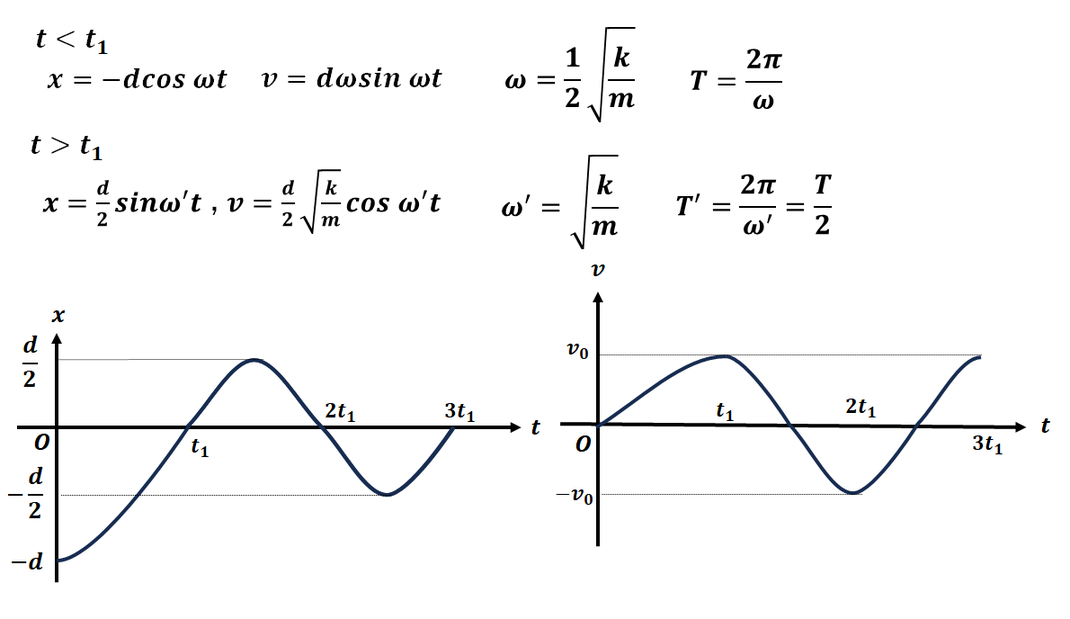
[1]、[2] の周期をそれぞれ計算し、
1 つのグラフにまとめて描きましょう。
なお、[2] のグラフは、
時刻
t = t_1t=t1 を時刻 0 として設定し、
その基準で式を立てて描画しています。

単振動パターンを使って解く場合の解答です。
必ずしも無理に使う必要はありませんが、
計算量を減らせるというメリットがあるため、
使い方に慣れておくと便利です。
運動方程式より、この運動は単振動であることがわかります。
初期条件が「バネをdだけ縮めて静かに離す」ことから、
これは位置確定パターンになります。
値があるのが位置(x=-d)なので,
xがcos関数になります。
速度は変位の時間微分をとって求めます。
3) は特徴位置でないので、xの関数から求めます。
4) は、中心位置なので初期位置から考えると、
単振動の1/4周期(T/4)になります。
5) 4)の速さ中心の速さが、最大速さになるので、
Aωもしくは、速さの式の最大位置から計算します。
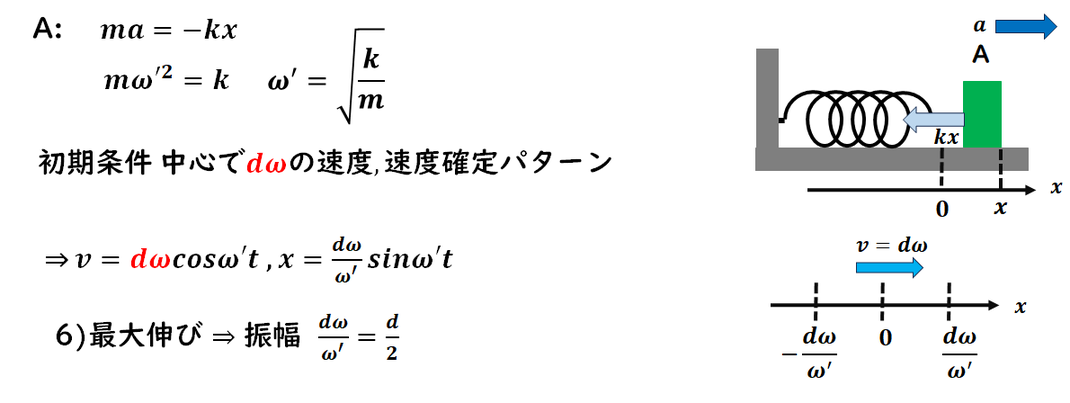
[2]の単振動は、
初期条件が「中心で、5)の速さを与える」ことから、
これは速度確定パターンになります。
値があるのが速度(v=dω)なので,
Vがcos関数になります。
xはvの積分(= 微分の逆)で求められます。
6)「最大の伸び」を求めることになるため、
これはすなわち振幅Aを求めることと同義です。
よって、xの式の係数がそのまま振幅になります。
d.[1]

つり合い時の運動方程式について
まず、物体 P、Q それぞれについて、
運動方程式を別々に立てましょう。
つり合いの状態では、PとQの間に働く垂直抗力N は
作用・反作用の関係にあります。
したがって、2つの運動方程式を足し合わせることで、
このN を打ち消すことができます。
その式を整理することで、
ばね定数k を求めることが可能になります。
運動中の運動方程式の立て方について
運動しているときの状況を正確に捉えるために、
P、Qを一体化した運動方程式を最初から作るのは避けましょう。
力学の基本姿勢:
1つの現象ごとに、それぞれ運動方程式を立てることが重要です。
そうすることで、以下のような力学の本質的理解が深まります。
-
それぞれの物体に働く力の向き・大きさを丁寧に整理できる
-
垂直抗力や張力、摩擦など、個別の力の扱いを見落とさずに済む
-
状況の変化(接触・分離など)にも柔軟に対応できる
力学では「現象ごとに運動方程式を立てる」という基本を徹底することで、
複雑な問題でも確実に・論理的に解ける力が身につきます。

この問題は少しややこしく感じるかもしれませんが、
ポイントはPやQそれぞれに働く外力を正しく見抜くことにあります。
それぞれの物体に注目し、
どのような力が加わっているのかを丁寧に整理したうえで、
個別に運動方程式を立てていきましょう。

各問題について解答していきます。
4) Pが離れない条件はN>0なので、
したがって、まずNを計算して
この条件を満たす範囲を求めます。
単振動は、「中心からb 縮める」単振動であり、
その最大位置はb になります。
このことから b<aが離れないための条件になります。
5) 周期はωの式から計算します。

離れるまでの運動は、
「中心からb 縮める」単振動なので、
位置確定パターンになります。
t=0で、x=-b=-2aなので、
xがcos関数になります。
速度は、xの微分で求められます。
6) 離れる位置は N=0より求まります。
7) 離れる位置の速度は6)の時間を
速度の関数に入れて計算します。

時間を複合して計算しても構いませんが、
運動の状態が変化するため、
物体が離れた時刻を新しい時間軸の始点として考えることにしましょう。
また、位置の基準も切り替え、
従来の x軸に対して、新たにX 軸を設定します。
ただし、最終的には元の軸に戻すことを忘れないようにしましょう。
したがって、複合的に計算しても問題はありませんが、
新しい軸で整理して考える方が、見通しがよくなります。
8) エネルギー保存則より最高高さを求めます。
運動エネルギー=-重力の仕事でも良いでしょう。
9) 離れた時間から最高位になるまでの時間を
速度の関係式から求めます。
力積の関係式 運動量の変化が重力×時間でも良いでしょう。
2つの運動の時間を足して計算します。
e.
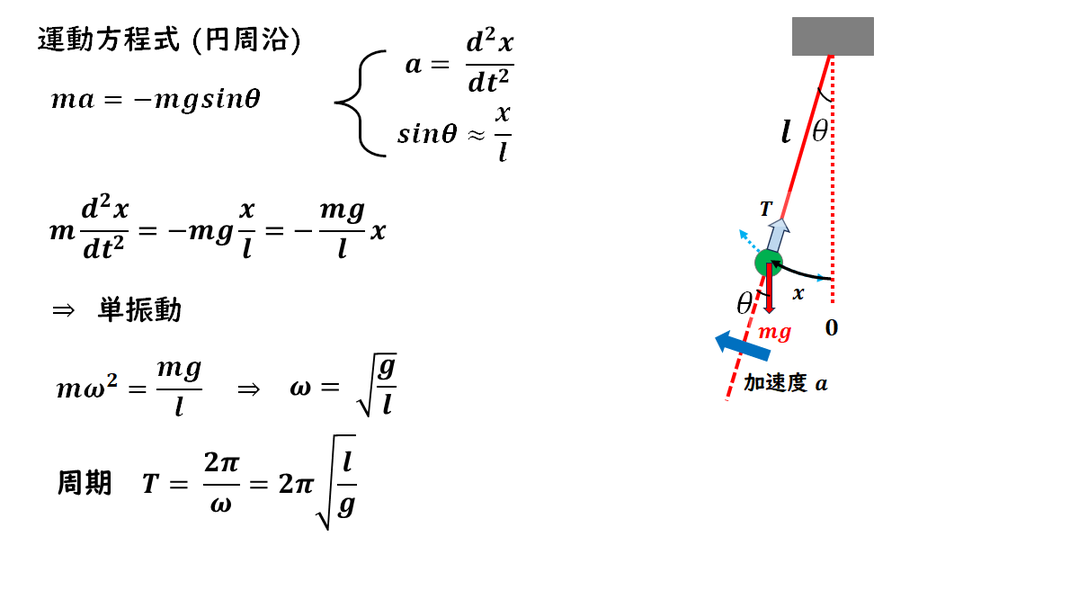
単振り子の問題で、周期を導く問題です。
1) 円運動の運動方程式を立てる際、
通常の向心方向ではなく、円周方向に注目して式を立てます。
このとき、円周方向に働く力は、重力 mg の円周方向成分だけになります。
2)角度θ が小さいとき、sinθ≈x/l という近似が使えます。
これを代入すると、運動方程式は単振動の形になります。
3)単振動の式から角加速度の関係を読み取り、
そこから角速度と周期を求めます。
周期については、基本公式なので、
しっかり覚えておきましょう。
