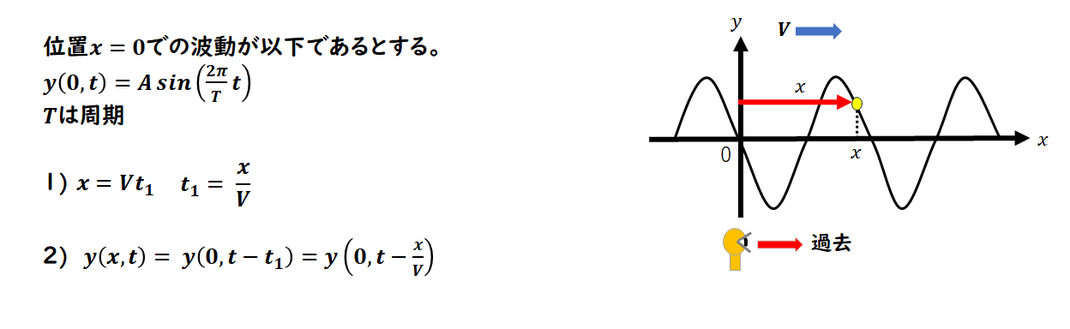波動入門
解説
すべてが必須問題です。
波動のグラフ、式、パラメータに
しっかりと慣れておきましょう。
これらの基本的な問題に
対応できるようになるだけでも、
多くの応用問題が解けるようになります。
自分の問題集や教科書を活用して、
しっかり確認しておきましょう。
a.

波動のパラメータに関する問題です。
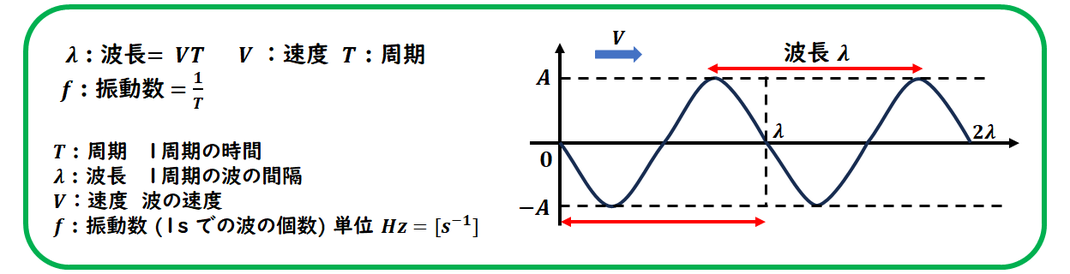
波長や速度の定義、
振動数の定義を正確に覚えましょう。
暗記するだけでなく、
振動数や波長といった物理的な感覚も
しっかりと身につけておくことが大切です。
1) 振動数は1sでの波の個数です。
周期Tで1個なので、
1sでの波の個数は 1/T になります。
f = 1/T ⇒ T = 1/f
2) λ = vTより求めます。

3),4) λ = vT , f = 1/T
より計算します。

5),6) λ = vT , f = 1/T
より計算します。
b.
1) ~ 4)
波動のグラフから
読み取る問題です。
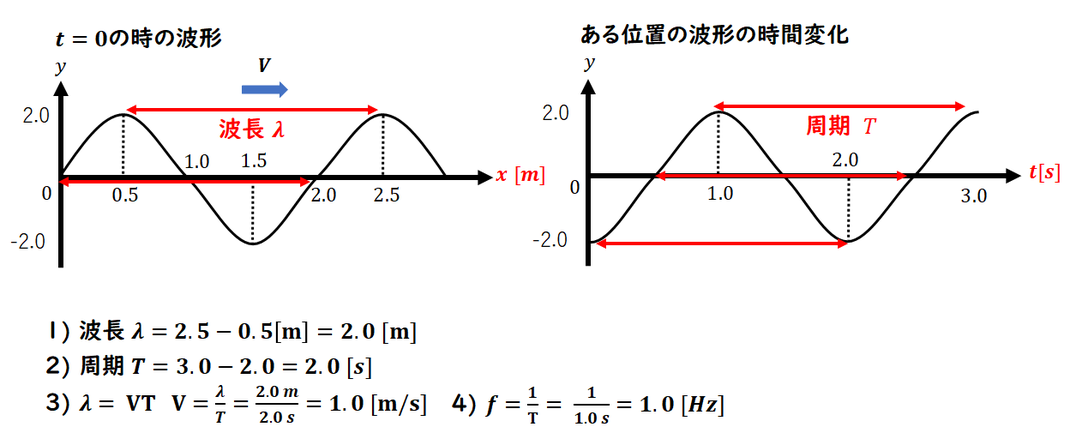
波動グラフの読み取りでは、
まず横軸の物理量を確認しましょう。
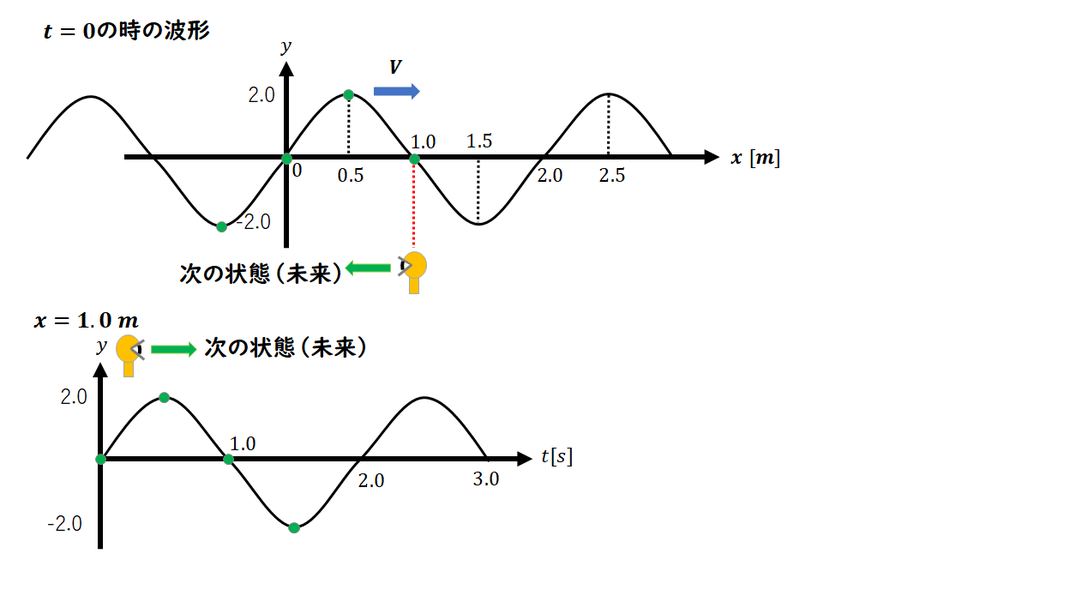
左の図は「位置」、
右の図は「時刻」を表しています。
1) 波長の読み取りについて
波長は「1周期の長さ」を意味するため、
左の図(位置グラフ)を使用します。
読み取りのポイントは、
ある位置での変位(y座標)が
再び同じ値になる場所までの距離です。
つまり、どの変位を基準に選んでも構いません。
その再現点との位置の差が波長になります。
このグラフから読み取ると、
波長は 2.0 m です。
2) 周期の読み取りについて
周期は「1周期の時間」を示すため、
右の図(時間グラフ)を利用します。
読み取り方法は、同じ変位(Y座標)になる
2つの時刻の差を測ることです。
どの変位を基準に選んでも構いません。
このグラフから読み取ると、
周期は 2.0 秒です。
3), 4) は、
波動のパラメータに関する計算問題です。
3) λ = vT より計算
4) f = 1/T より計算
します。
5)
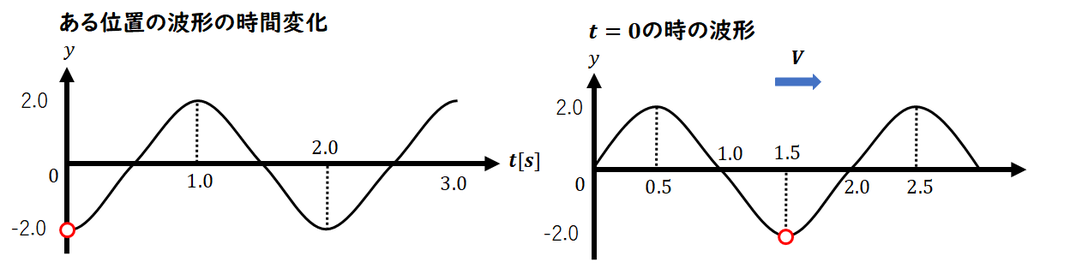
ある位置を求める問題です。
位置のグラフは t = 0 の
時刻を表しているため、
このときの 変位 Y の値から、
該当する 位置 X を特定します。
時刻のグラフから、t = 0 では
Y = -2.0 であることがわかります。
この変位 Y = -2.0 となる位置を、
位置のグラフから読み取ると、
X = 1.5 m であることがわかります。
6)
x = 1.0 m における
時間変化のグラフについて
波の速度が正(正の向きに進行)
であるため、
負の方向(左側)から
波がやってくることになります。
この点をまず理解しましょう。
x = 1.0 m において、
波がやってくる方向
(x < 1.0 m)を見て、
その変位の時間変化を
グラフに描きます。
波の中心、振幅の位置を
目安にしてグラフを
描くとよいでしょう。
周期は2.0s とした
グラフを描きましょう。
c.
単振動の位置が
波のどこに対応するかを問う問題です。
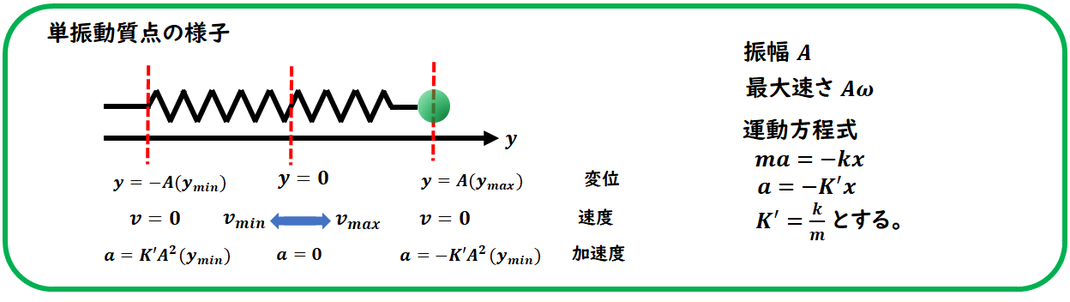
まず、単振動における
位置・速度・加速度の関係を
しっかり復習しておきましょう。
このタイプの問題では、特に
速度が最大・最小となる位置が頻出です。
意味を理解したうえで、
納得して覚えておくことが大切です。
また、加速度に関する出題も
時折見られますので、
こちらも合わせて確認しておきましょう。
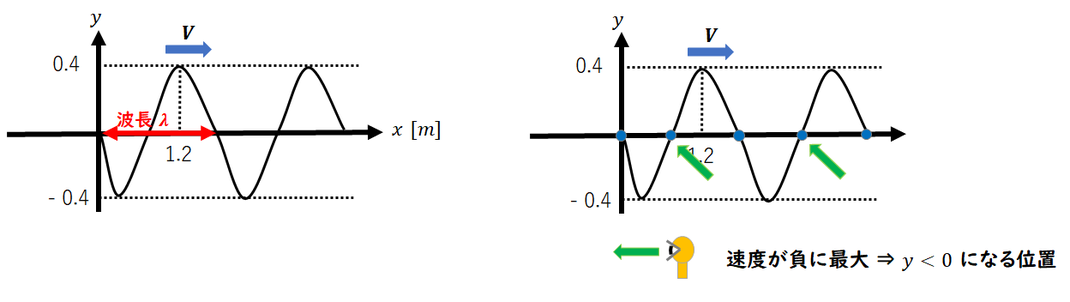
まず、横軸が位置
のグラフであることを
認識してください。
未来は、-x方向になります。
1) 振幅
最大y位置の事なので、
y最大=0.4mです。
2)波長
1周期分の長さです。
そのままは
読み取れないようになっています。
3/4 λ 分 = 1.2mと読み取れれば、
1/4 λ = 1.2 / 3 = 0.4mより、
λ = 1.6 m です。
3) 速度の位置です。
負最大⇒その後、
yの位置が最小となる
中心位置が求める位置です。
未来の方向を考えれば、
0.8 , 2.4 m となります。
横軸が時刻です。
未来は、+x方向です。
4) 振動数 f = 1/Tより
周期Tが分かれば、
良いことになります。
Tを読み取ると、
0.2sです。
f = 5 Hz になります。
5) 振幅はy最大位置なので、
0.7mです。
6) 速度です。
負最大なので、
その後、
yの位置が最小となる
中心位置が求める位置です。
未来の方向は、+xなので、
0.2,0.4s の時になります。
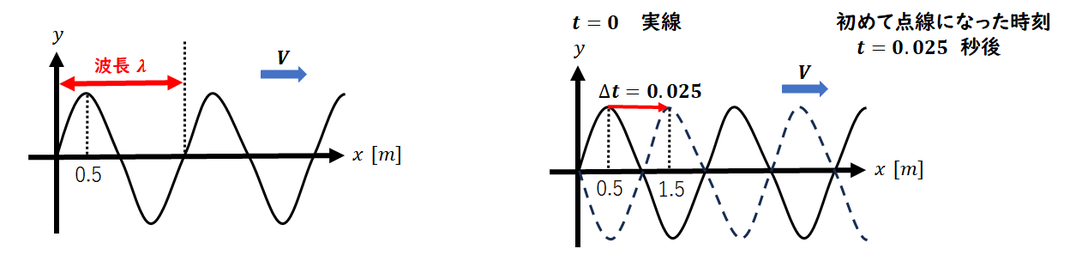
横軸は位置のグラフです。
実際に移動した波も
一緒に描かれています。
黒線が点線まで移動した
事を理解してください。
7) 波長
読み取ればよいのですが、
1/4λ 分が読み取れます。
λ = 0.5 × 4 = 2.0 m です。
8) 移動距離、移動時間から
速度を計算します。
問題より
移動時間Δt = 0.025 s
移動距離は
どこの点でも良く、
実線を実際に
速度方向に移動して
点線に当たった位置が
移動距離になります。
読み取れる位置を
選択する必要があり、
山の頂上の点を選んで、
Δx = 1.5 - 0.5 = 1.0 m
とわかります。
V = Δx / Δt = 40 m/s
になります。
9) 10) 波動のパラメータなので、
計算間違えしないようにして求めます。
d.
反射する波での
合成波を作図する問題です。
手順を覚えましょう。
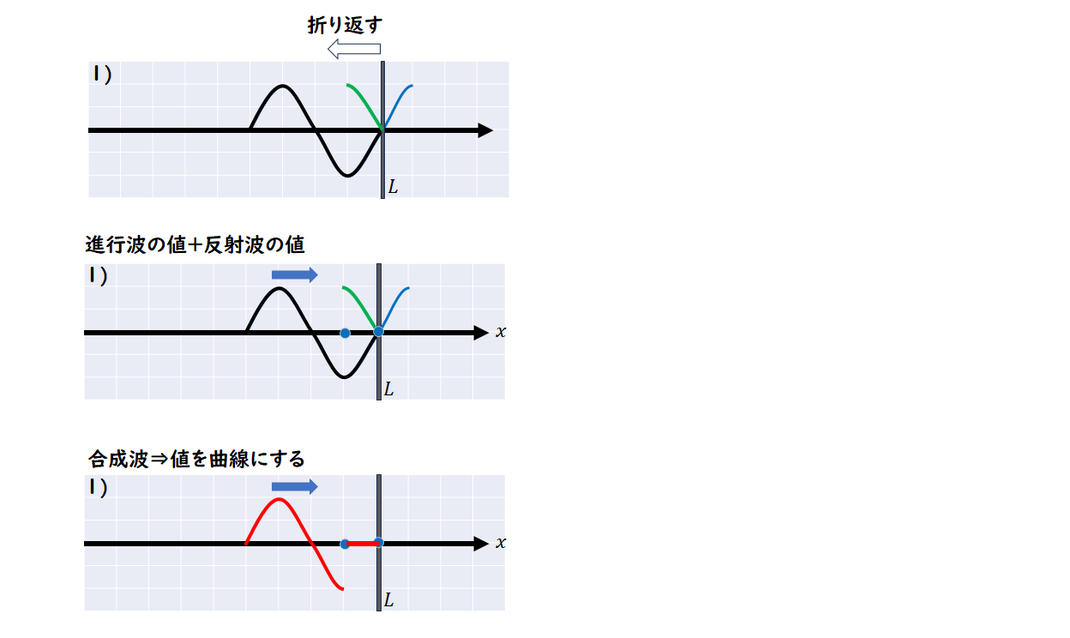
1) 自由端反射の場合
自由端反射の場合の反射波は、
通過波を折り返して作成します。
合成波は各値を足して値を求めます。
どちらかが0となる位置を
必ず使います。
あとは、両方の値が分かれば、
その位置も利用します。
わかる点を曲線で結んで、
合成波を作図します。
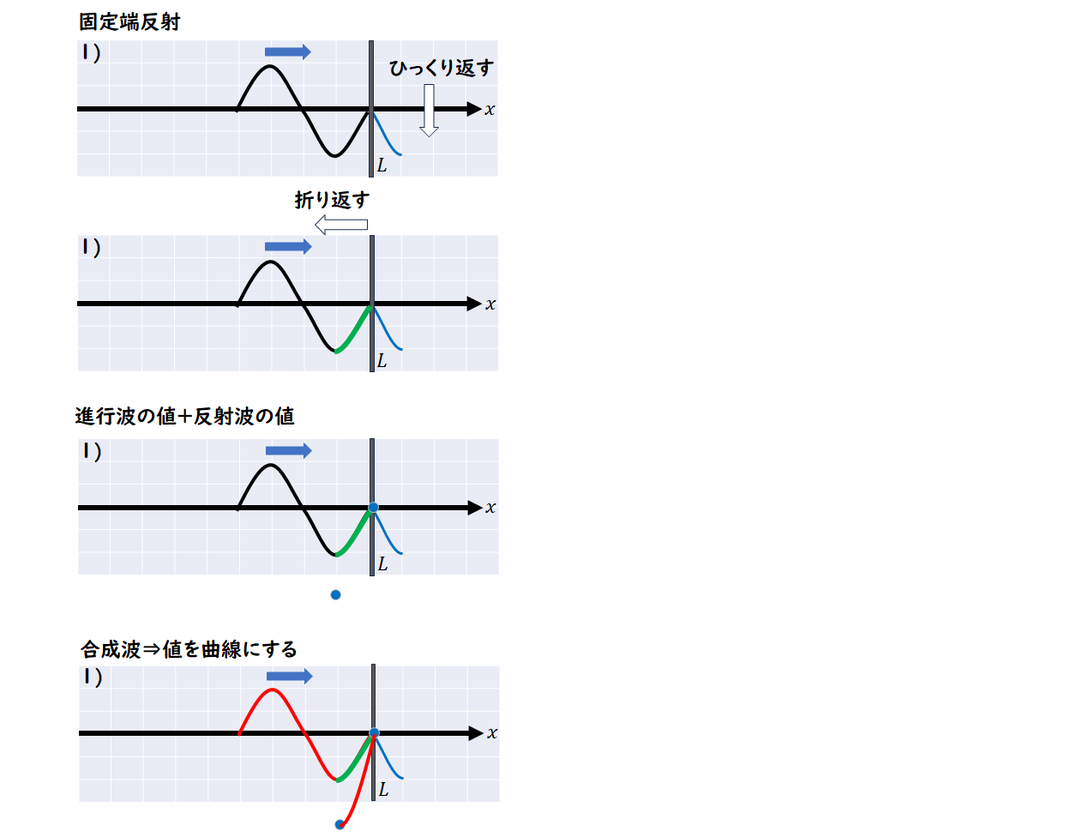
固定端反射の場合
固定端反射の場合の反射波は、
通過波をひっくり返して
折り返すことで作成します。
合成波は各値を足して値を求めます。
自由端反射の場合との違いは、
最初のひっくり返す作業だけです。
後は同じです。
2),3)も同じです。
間違えないように作図してみましょう。
2)
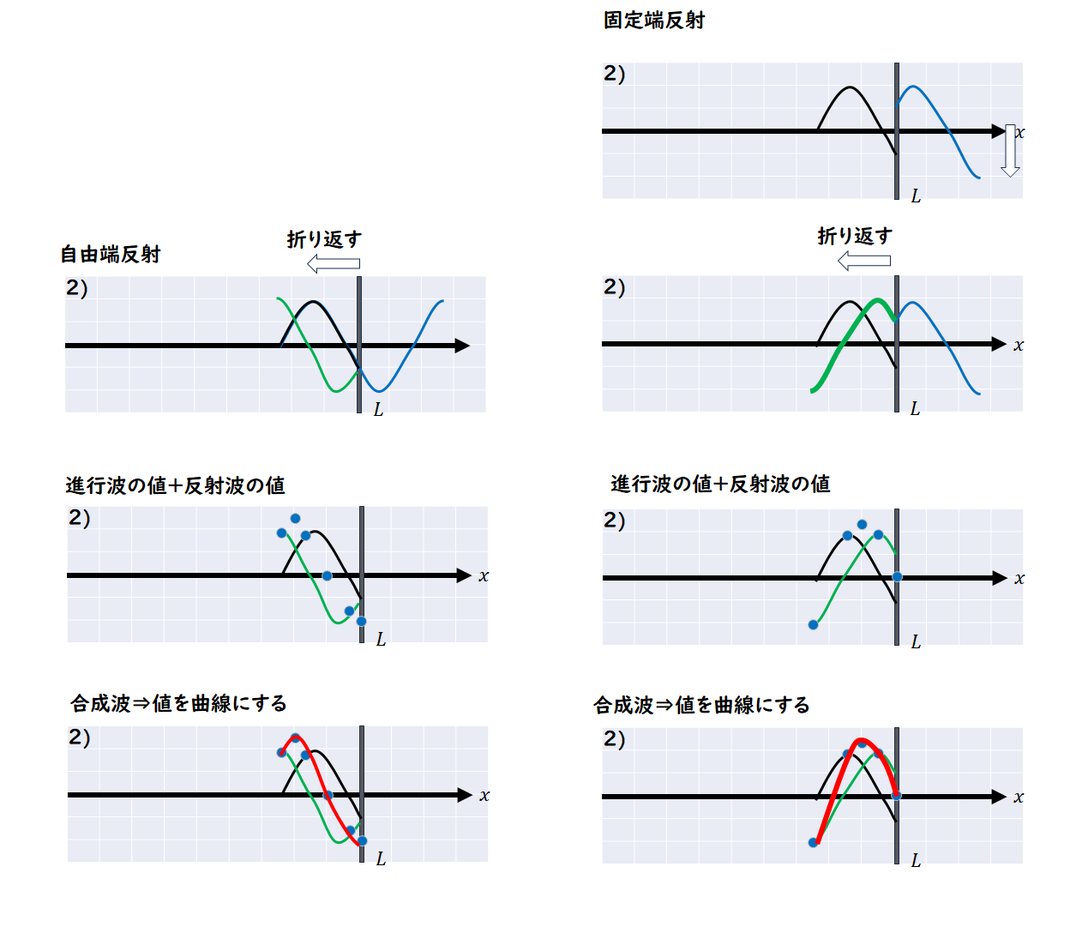
3)
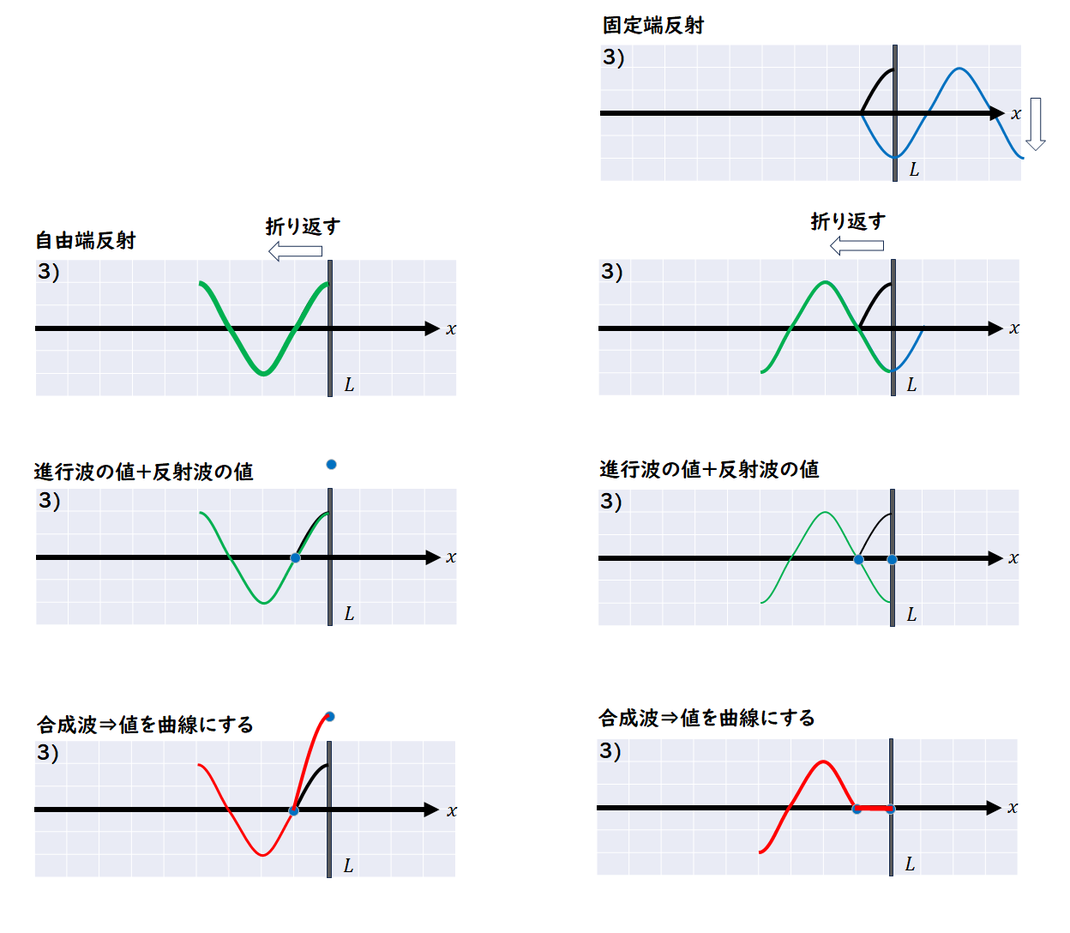
固定端反射の場合は、
ひっくり返す作業が追加されます。
後は同じ作業です。
固定端反射の場合の合成波は
反射位置で節(=0)になることを
覚えておきましょう。
0になっていない場合は
作図は間違えということになります。
e.
波動の式の問題です。
何回か演習すれば、
覚えられるので、
やってみましょう。
[1]
ある位置の
時間変化がわかる時の
位置xでの波動の式を
求める問題です。
この問題のある位置はx=0です。
1) 位置xまでの時間を求める問題です。
波の速度はVなので、
x=Vt1
より時間が求まります。
2) 1)の時間がわかったので、
xの位置の時間変化を求めます。
何をすればよいのかというと、
xの位置は原点の位置で考えるといつと同じなのか?
を式で表せばよいということです。
xまでに時間t1かかります。
xの位置はx=0から見ると、t1過去になります。
波の左からやってくるので。
ということは、t1過去 t1遅れることになります。
これを式にすればよく、
y(x,t):位置x,時刻tの波動
= y(0,t-t1):位置x=0での、位置xの波動
になります。
y(x,t)= y(0,t-t1)
を理解できれば良いことになります。
あとは、式にいれて計算すればよいです。
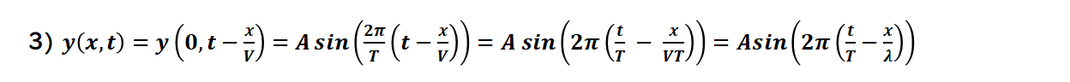
式に入れて、計算します。
λ=VTはパラメータ計算です。
この出題方式が基本で、多いです。
[2]
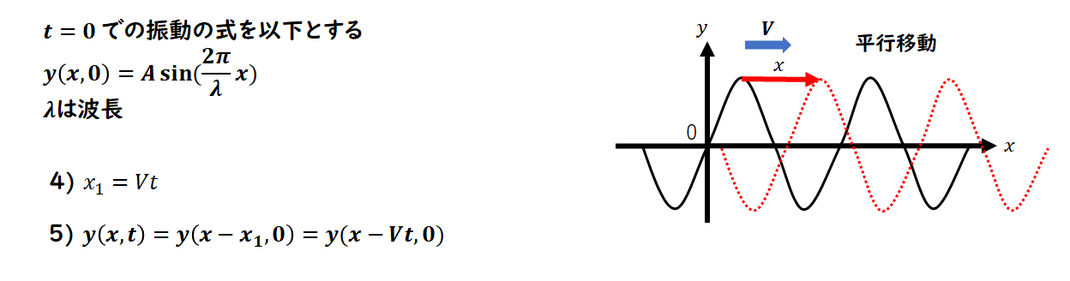
[1]と似ていますが
t=0の波動がわかっている問題です。
4) x1までの時間を求めます。
x1= Vtです。
5) 位置がわかっている場合は、
平行移動すればよいです。
y(x,0)をx1分速度方向(x=x1まで)に
平行移動するには、
y(x-x1,0)です。
数式処理です。
y(x,t) = y(x-x1,0)
になります。
後は同じように計算して求めます。
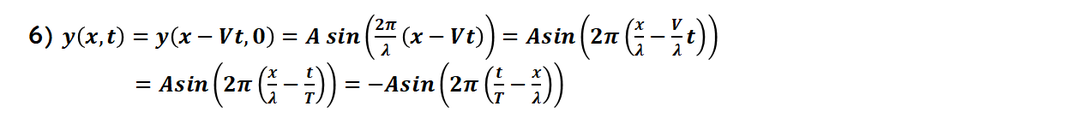
最後、-を外に出していますが、
出さなくても正解です。
絶対に間違えてはいけない
入門レベルの問題です。
何度か繰り返せば、
しっかり理解できるようになります。
もし曖昧なまま覚えていたなら、
ここでしっかり整理して覚えてください。
この内容だけでも、
かなり多くの問題に対応できるはずです。
中間・期末テストレベルであれば、
少しの追加知識(プラスアルファ)で
十分対応できます。